Revisiting the basic reproductive number for malaria and its implications for malaria control

Abstract

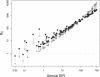
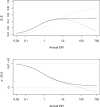
The prospects for the success of malaria control depend, in part, on the basic reproductive number for malaria, R0. Here, we estimate R0 in a novel way for 121 African populations, and thereby increase the number of R0 estimates for malaria by an order of magnitude. The estimates range from around one to more than 3,000. We also consider malaria transmission and control in finite human populations, of size H. We show that classic formulas approximate the expected number of mosquitoes that could trace infection back to one mosquito after one parasite generation, Z0(H), but they overestimate the expected number of infected humans per infected human, R0(H). Heterogeneous biting increases R0 and, as we show, Z0(H), but we also show that it sometimes reduces R0(H); those who are bitten most both infect many vectors and absorb infectious bites. The large range of R0 estimates strongly supports the long-held notion that malaria control presents variable challenges across its transmission spectrum. In populations where R0 is highest, malaria control will require multiple, integrated methods that target those who are bitten most. Therefore, strategic planning for malaria control should consider R0, the spatial scale of transmission, human population density, and heterogeneous biting.

Figure 1. The Life Cycle Model and R ₀

The basic reproductive number, R ₀, is derived by computing the expected number of vertebrate hosts or vectors that would be infected through one complete generation of the parasite by a single infected mosquito or a single infected human. The underlying mathematical model, by Ross [11] and Macdonald [12] and with a slight modification by Smith and McKenzie [27], is a quantitative description of the idealized life cycle. This diagram follows one by Macdonald et al. [23]. The parameters are described in Table 2.

Figure 2. R ₀ Estimates for 121 African Populations

Here, we show two different sets of estimates, plotted as a function of the estimated EIR. The first set of estimates assumes that none of the parameter estimates are biased by immunity or heterogeneous biting at the equilibrium (solid circles). The second set of estimates assumes that heterogeneous biting and transmission-blocking immunity bias parameters (open circles); σ is as illustrated by Figure 3. Corrections for this potential bias substantially increase the range of R ₀ estimates.

Figure 3. The Index of Sampling Bias, σ

(Top) The PR (grey line) rises monotonically with EIR. The fraction of mosquitoes that become infected after biting a human, X~, is initially higher than the PR because of heterogeneous biting, but at high EIR, PR continues to rise while X~ remains flat without transmission-blocking immunity (solid black line) or declines with it (dashed line). (Bottom) Without transmission-blocking immunity, the index of sampling bias, σ, declines from near c ₀(1 + α) to c ₀ (solid black line). At low EIR, the estimates of PR from a well-designed study underestimate the probability a mosquito becomes infected. At high EIR, without transmission-blocking immunity, this bias becomes insignificant. At high EIR, with transmission-blocking immunity, the PR in children substantially overestimates infectivity (dashed line). These graphs assume heterogeneous biting and model transmission-blocking immunity as in equation 20, with γ = 0.001 (Methods).

Figure 4. R ₀, R ₀(H), and Z ₀(H) in Finite Populations

In finite populations, the number of different hosts infected through one complete generation of the parasite differs when the counting starts with humans, R ₀(H) (black circles, solid line), or with mosquitoes, Z ₀(H) (grey circles, dashed line), because of the different proportion of reinfected humans and mosquitoes (represented by boxes 1–4 with asterisks). These expectations are computed with heterogeneous biting, where individual biting rates differ from the average by the factor s_i, called the biting weight (Methods). Box 1: for humans, a fraction of bites come from mosquitoes that were already infected (≈H/[H + cS]). Box 2: when these bites arrive back on a finite human population, they are distributed among the humans; some humans are bitten many times. The incidence of repeat infection is higher when R ₀ exceeds H. Box 3: starting with a single infectious mosquito, some fraction of humans become infected (less than bS), possibly more than once. Box 4: this affects the number of mosquitoes that are reinfected from biting the humans infected by a single mosquito (less than H/[H + bcS ²]). Explicit formulas are given in the Methods.

Figure 5. R ₀(H) and Z ₀(H) in Finite Populations with Heterogeneous and Uniform Biting at Three Biting Intensities

The three biting intensities shown are for an R ₀ for homogenous biting equal to 10 (top), 50 (middle), and 250 (bottom). R ₀(H) rises slowly to R ₀, as a function of H, whether biting rates are heterogeneous (solid black lines) or uniform (dashed lines). Surprisingly, R ₀(H) for heterogeneous biting is lower than that for uniform biting, especially when H is low and R ₀ is high. By contrast, Z ₀(H) rises rapidly to R ₀ as a function of human population size, H, when biting rates are heterogeneous (dotted lines) or completely uniform (grey lines). These effects occur at population sizes well below those where the transmission-reducing effects of urbanization are evident [3].

Figure 6. Achieving Herd Immunity with Random and Targeted Intervention

This figure shows the relationship between R ₀ and the proportion of a population that must be neutralized through chemoprophylaxis or a vaccine if the intervention is perfectly targeted (solid lines) or random (dashed lines), such that R ₀ < 1. As the population size increases (from 20 to 50 to 100), the proportion that must be vaccinated increases for random intervention, but not for intervention targeted towards those bitten most.

Figure 7. Changes in Transmission in Finite Populations with Heterogeneous Biting under Control by ITNs or IRS

(A) In a population with 20% coverage, total biting decreases, but some bites are redistributed, so biting increases on those who are unprotected. The baseline biting weights (solid black line) are plotted, along with the comparable post-control biting weights after targeted (solid grey) and random (dashed) ITN distribution or IRS application. (B) ITNs or IRS reduce transmission more efficiently when they are targeted. (Here, R ₀ = 40, R ₀(H) ≈ 34, and Z ₀(H) ≈ 172.) For example, 10% targeted coverage (blue lines) and 70% random coverage (black lines; the solid line is the median and the dotted lines show the fifth and 95th quantiles) reduce Z ₀(H) (the lines that originate at 172) by about the same amount at the median. For these parameters, 100% coverage is required to reduce R ₀(H) below one, so for higher R ₀ values, 100% ITN or IRS coverage would be insufficient to eliminate malaria.