Variability in stepping direction explains the veering behavior of blind walkers
- PMID: 17311487
- PMCID: PMC2259118
- DOI: 10.1037/0096-1523.33.1.183
Variability in stepping direction explains the veering behavior of blind walkers
Abstract
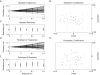
Walking without vision results in veering, an inability to maintain a straight path that has important consequences for blind pedestrians. In this study, the authors addressed whether the source of veering in the absence of visual and auditory feedback is better attributed to errors in perceptual encoding or undetected motor error. Three experiments had the following results: No significant differences in the shapes of veering trajectories were found between blind and blindfolded participants; accuracy in detecting curved walking paths was not correlated with simple measures of veering behavior; and explicit perceptual cues to initial walking direction did not reduce veering. The authors present a model that accounts for the major characteristics of participants' veering behavior by postulating 3 independent sources of undetected motor error: initial orientation, consistent biases in step direction, and, most important, variable error in individual steps.
Figures

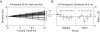
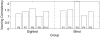






References
-
- Bauby CE, Kuo AD. Active control of lateral balance in human walking. Journal of Biomechanics. 2000;33:1433–1440. - PubMed
-
- Chance SS, Gaunet F, Beall AC, Loomis JM. Locomotion mode affects the updating of objects encountered during travel: The contribution of vestibular and proprioceptive inputs to path integration. Presence-Teleoperators and Virtual Environments. 1998;7:168–178.
-
- Cicinelli JG. Master's Thesis. Department of Psychology, University of California; Santa Barbara: 1989. Veer as a function of preview and walking speed.
-
- Cohen HS. Vestibular disorders and impaired path integration along a linear trajectory. Journal of Vestibular Research. 2000;10:7–15. - PubMed
-
- Cratty BJ. Perceptual thresholds of non-visual locomotion (Part 1) Los Angeles: University of California; 1965.

