Persistent activity in neural networks with dynamic synapses
- PMID: 17319739
- PMCID: PMC1808024
- DOI: 10.1371/journal.pcbi.0030035
Persistent activity in neural networks with dynamic synapses
Erratum in
- PLoS Comput Biol. 2007 Mar;3(3):e70
Abstract
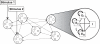
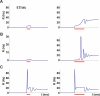
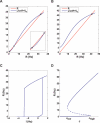
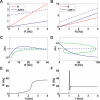
Persistent activity states (attractors), observed in several neocortical areas after the removal of a sensory stimulus, are believed to be the neuronal basis of working memory. One of the possible mechanisms that can underlie persistent activity is recurrent excitation mediated by intracortical synaptic connections. A recent experimental study revealed that connections between pyramidal cells in prefrontal cortex exhibit various degrees of synaptic depression and facilitation. Here we analyze the effect of synaptic dynamics on the emergence and persistence of attractor states in interconnected neural networks. We show that different combinations of synaptic depression and facilitation result in qualitatively different network dynamics with respect to the emergence of the attractor states. This analysis raises the possibility that the framework of attractor neural networks can be extended to represent time-dependent stimuli.
Conflict of interest statement
Figures
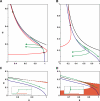


References
-
- Fuster JM, Alexander GE. Neuron activity related to short-term memory. Science. 1971;173:652–654. - PubMed
-
- Miyashita Y. Neuronal correlate of visual associative long-term memory in the primate temporal cortex. Nature. 1988;335:817–820. - PubMed
-
- Goldman-Rakic PS. Cellular basis of working memory. Neuron. 1995;14:477–485. - PubMed
-
- Amit DJ. Modelling brain function. New York: Cambridge University Press; 1989. 504
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Medical

