Factor analysis for gene regulatory networks and transcription factor activity profiles
- PMID: 17319944
- PMCID: PMC1821042
- DOI: 10.1186/1471-2105-8-61
Factor analysis for gene regulatory networks and transcription factor activity profiles
Abstract
Background: Most existing algorithms for the inference of the structure of gene regulatory networks from gene expression data assume that the activity levels of transcription factors (TFs) are proportional to their mRNA levels. This assumption is invalid for most biological systems. However, one might be able to reconstruct unobserved activity profiles of TFs from the expression profiles of target genes. A simple model is a two-layer network with unobserved TF variables in the first layer and observed gene expression variables in the second layer. TFs are connected to regulated genes by weighted edges. The weights, known as factor loadings, indicate the strength and direction of regulation. Of particular interest are methods that produce sparse networks, networks with few edges, since it is known that most genes are regulated by only a small number of TFs, and most TFs regulate only a small number of genes.
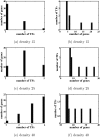
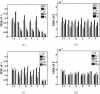
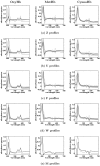
Results: In this paper, we explore the performance of five factor analysis algorithms, Bayesian as well as classical, on problems with biological context using both simulated and real data. Factor analysis (FA) models are used in order to describe a larger number of observed variables by a smaller number of unobserved variables, the factors, whereby all correlation between observed variables is explained by common factors. Bayesian FA methods allow one to infer sparse networks by enforcing sparsity through priors. In contrast, in the classical FA, matrix rotation methods are used to enforce sparsity and thus to increase the interpretability of the inferred factor loadings matrix. However, we also show that Bayesian FA models that do not impose sparsity through the priors can still be used for the reconstruction of a gene regulatory network if applied in conjunction with matrix rotation methods. Finally, we show the added advantage of merging the information derived from all algorithms in order to obtain a combined result.
Conclusion: Most of the algorithms tested are successful in reconstructing the connectivity structure as well as the TF profiles. Moreover, we demonstrate that if the underlying network is sparse it is still possible to reconstruct hidden activity profiles of TFs to some degree without prior connectivity information.
Figures
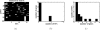





References
-
- Ming H, Abuja N, Kriegman D. Face detection using mixtures of linear subspaces. Proceedings Fourth International Conference on Automatic Face and Gesture Recognition. 2000;4:70–76.
-
- Aguilar O, West M. Bayesian dynamic factor models and portfolio allocation. Journal of Business and Economic Statistics. 2000;18:338–357.
-
- West M. Bayesian factor regression models in the "Large p, Small n" paradigm. Bayesian statistics. 2003;7:733–742.
-
- Sabatti C, James G. Bayesian sparse hidden components analysis for transcription regulation networks. Bioinformatics. 2006;22:739–746. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

