Strong effects of molecular topology on diffusion of entangled DNA molecules

Abstract

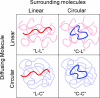
When long polymers such as DNA are in a highly concentrated state they may become entangled, leading to restricted self-diffusion. Here, we investigate the effect of molecular topology on diffusion in concentrated DNA solutions and find surprisingly large effects, even with molecules of modest length and concentration. We measured the diffusion coefficients of linear and relaxed circular molecules by tracking the Brownian motion of single molecules with fluorescence microscopy. Four possible cases were compared: linear molecules surrounded by linear molecules, circular molecules surrounded by linear molecules, linear molecules surrounded by circles, and circles surrounded by circles. In measurements with 45-kbp DNA at 1 mg/ml, we found that circles diffused approximately 100 times slower when surrounded by linear molecules than when surrounded by circles. In contrast, linear and circular molecules diffused at nearly the same rate when surrounded by circles, and circles diffused approximately 10 times slower than linears when surrounded by linears. Thus, diffusion in entangled DNA solutions strongly depends on topology of both the diffusing molecule and the surrounding molecules. This effect also strongly depends on DNA concentration and length. The differences largely disappeared when the concentration was lowered to 0.1 mg/ml or when the DNA length was lowered to 6 kb. Present theories cannot fully explain these effects.

Fig. 1.

Schematic illustration of the possible topological combinations of entangled linear and relaxed circular DNA molecules. The four cases depicted are: a linear diffusing molecule surrounded by linear molecules (L-L), circular molecule surrounded by linear molecules (C-L), linear molecule surrounded by circular molecules (L-C), and circular molecule surrounded by circular molecules (C-C). Linear molecules are shaded red, and circular molecules are blue. For clarity, the diffusing molecules are represented by brighter, thicker lines than the surrounding molecules.

Fig. 2.

Dependence of DNA self-diffusion coefficients (D) on molecular topology. Bar graphs display normalized D values vs. topological case (shown in Fig. 1). All D values are normalized by the corresponding measured diffusion coefficient for a circular DNA surrounded by circular DNA (D_C-C) (the highest value of D in each case). The DNA length and concentration is listed in each plot.

Fig. 3.

Schematic model of the effect of increasing length and concentration on the conformation and diffusion of a circular DNA molecule. Black dots represent “obstacles” formed by surrounding entangled DNA molecules, and the blue loop represents a diffusing circular DNA. (a–d) The effect of increasing the molecular length, as proposed in ref. . (e–h) The effect of increasing concentration. With short length (a) or low concentration (e), the molecule is most likely unthreaded and can diffuse by reptation. As length (c and d) or concentration (f–h) increases, DNA is increasingly likely to get threaded and can only diffuse by constraint release of the surrounding entangling DNA.