Modeling networks of coupled enzymatic reactions using the total quasi-steady state approximation
- PMID: 17367203
- PMCID: PMC1828705
- DOI: 10.1371/journal.pcbi.0030045
Modeling networks of coupled enzymatic reactions using the total quasi-steady state approximation
Abstract
In metabolic networks, metabolites are usually present in great excess over the enzymes that catalyze their interconversion, and describing the rates of these reactions by using the Michaelis-Menten rate law is perfectly valid. This rate law assumes that the concentration of enzyme-substrate complex (C) is much less than the free substrate concentration (S0). However, in protein interaction networks, the enzymes and substrates are all proteins in comparable concentrations, and neglecting C with respect to S0 is not valid. Borghans, DeBoer, and Segel developed an alternative description of enzyme kinetics that is valid when C is comparable to S0. We extend this description, which Borghans et al. call the total quasi-steady state approximation, to networks of coupled enzymatic reactions. First, we analyze an isolated Goldbeter-Koshland switch when enzymes and substrates are present in comparable concentrations. Then, on the basis of a real example of the molecular network governing cell cycle progression, we couple two and three Goldbeter-Koshland switches together to study the effects of feedback in networks of protein kinases and phosphatases. Our analysis shows that the total quasi-steady state approximation provides an excellent kinetic formalism for protein interaction networks, because (1) it unveils the modular structure of the enzymatic reactions, (2) it suggests a simple algorithm to formulate correct kinetic equations, and (3) contrary to classical Michaelis-Menten kinetics, it succeeds in faithfully reproducing the dynamics of the network both qualitatively and quantitatively.
Conflict of interest statement
Figures



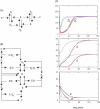
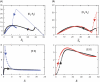
References
-
- Bray D. Protein molecules as computational elements in living cells. Nature. 1995;376:307–312. - PubMed
-
- Hartwell LH, Hopfield JJ, Leibler S, Murray AW. From molecular to modular cell biology. Nature. 1999;402:C47–C52. - PubMed
-
- Tyson JJ, Chen K, Novak B. Network dynamics and cell physiology. Nat Rev Mol Cell Biol. 2001;2:908–916. - PubMed
-
- Tyson JJ, Novak B, Odell GM, Chen K, Thron CD. Chemical kinetic theory: Understanding cell-cycle regulation. Trends Biochem Sci. 1996;21:89–96. - PubMed
-
- Segel LA. On the validity of the steady state assumption of enzyme kinetics. Bull Math Biol. 1988;50:579–593. - PubMed
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Miscellaneous

