Scale-invariant memory representations emerge from moiré interference between grid fields that produce theta oscillations: a computational model
- PMID: 17376982
- PMCID: PMC6672484
- DOI: 10.1523/JNEUROSCI.4724-06.2007
Scale-invariant memory representations emerge from moiré interference between grid fields that produce theta oscillations: a computational model
Abstract
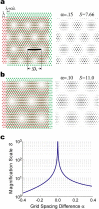
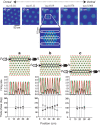
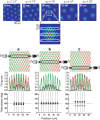
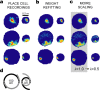
The dorsomedial entorhinal cortex (dMEC) of the rat brain contains a remarkable population of spatially tuned neurons called grid cells (Hafting et al., 2005). Each grid cell fires selectively at multiple spatial locations, which are geometrically arranged to form a hexagonal lattice that tiles the surface of the rat's environment. Here, we show that grid fields can combine with one another to form moiré interference patterns, referred to as "moiré grids," that replicate the hexagonal lattice over an infinite range of spatial scales. We propose that dMEC grids are actually moiré grids formed by interference between much smaller "theta grids," which are hypothesized to be the primary source of movement-related theta rhythm in the rat brain. The formation of moiré grids from theta grids obeys two scaling laws, referred to as the length and rotational scaling rules. The length scaling rule appears to account for firing properties of grid cells in layer II of dMEC, whereas the rotational scaling rule can better explain properties of layer III grid cells. Moiré grids built from theta grids can be combined to form yet larger grids and can also be used as basis functions to construct memory representations of spatial locations (place cells) or visual images. Memory representations built from moiré grids are automatically endowed with size invariance by the scaling properties of the moiré grids. We therefore propose that moiré interference between grid fields may constitute an important principle of neural computation underlying the construction of scale-invariant memory representations.
Figures




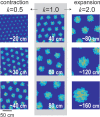

References
-
- Amidror I. The theory of the moiré phenomenon. Kluwer Academic; 2000.
-
- Biederman I, Cooper EE. Size invariance in visual object priming. J Exp Psychol Hum Percept Perform. 1992;18:121–133.
-
- Brown MW, Aggleton JP. Recognition memory: what are the roles of the perirhinal cortex and hippocampus? Nat Rev Neurosci. 2001;2:51–61. - PubMed
-
- Burgess N, Barry C, Jefferies KJ, O'Keefe J. A grid and place cell model of path integration utilizing phase precession versus theta. 1st Annual Conference on Computational Cognitive Neuroscience; Washington, DC. 2005.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
