The impact of input fluctuations on the frequency-current relationships of layer 5 pyramidal neurons in the rat medial prefrontal cortex
- PMID: 17376988
- PMCID: PMC6672485
- DOI: 10.1523/JNEUROSCI.4937-06.2007
The impact of input fluctuations on the frequency-current relationships of layer 5 pyramidal neurons in the rat medial prefrontal cortex
Abstract
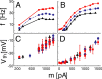
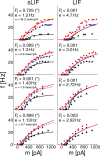
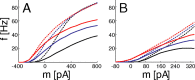
The role of irregular cortical firing in neuronal computation is still debated, and it is unclear how signals carried by fluctuating synaptic potentials are decoded by downstream neurons. We examined in vitro frequency versus current (f-I) relationships of layer 5 (L5) pyramidal cells of the rat medial prefrontal cortex (mPFC) using fluctuating stimuli. Studies in the somatosensory cortex show that L5 neurons become insensitive to input fluctuations as input mean increases and that their f-I response becomes linear. In contrast, our results show that mPFC L5 pyramidal neurons retain an increased sensitivity to input fluctuations, whereas their sensitivity to the input mean diminishes to near zero. This implies that the discharge properties of L5 mPFC neurons are well suited to encode input fluctuations rather than input mean in their firing rates, with important consequences for information processing and stability of persistent activity at the network level.
Figures




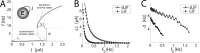

References
-
- Ahmed B, Anderson JC, Douglas RJ, Martin KA, Whitteridge D. Estimates of the net excitatory currents evoked by visual stimulation of identified neurons in cat visual cortex. Cereb Cortex. 1998;8:462–476. - PubMed
-
- Amit DJ, Brunel N. Model of global spontaneous activity and local structured activity during delay periods in the cerebral cortex. Cereb Cortex. 1997a;7:237–252. - PubMed
-
- Amit DJ, Brunel N. Dynamics of a recurrent network of spiking neurons before and following learning. Netw Comput Neural Syst. 1997b;8:373–404.
-
- Brette R, Gerstner W. Adaptive exponential integrate-and-fire model as an effective description of neuronal activity. J Neurophysiol. 2005;94:3637–3642. - PubMed
-
- Brody CD, Romo R, Kepecs A. Basic mechanisms for graded persistent activity: discrete attractors, continuous attractors, dynamic representations. Curr Opin Neurobiol. 2003;13:204–211. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Molecular Biology Databases
