From single-cell genetic architecture to cell population dynamics: quantitatively decomposing the effects of different population heterogeneity sources for a genetic network with positive feedback architecture

Abstract

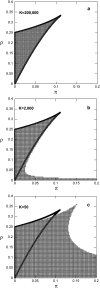
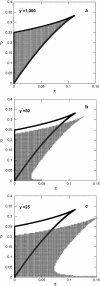
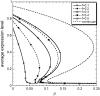
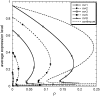
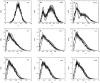
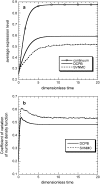
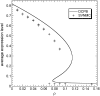
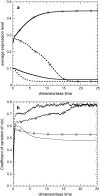
Phenotypic cell-to-cell variability or cell population heterogeneity originates from two fundamentally different sources: unequal partitioning of cellular material at cell division and stochastic fluctuations associated with intracellular reactions. We developed a mathematical and computational framework that can quantitatively isolate both heterogeneity sources and applied it to a genetic network with positive feedback architecture. The framework consists of three vastly different mathematical formulations: a), a continuum model, which completely neglects population heterogeneity; b), a deterministic cell population balance model, which accounts for population heterogeneity originating only from unequal partitioning at cell division; and c), a fully stochastic model accommodating both sources of population heterogeneity. The framework enables the quantitative decomposition of the effects of the different population heterogeneity sources on system behavior. Our results indicate the importance of cell population heterogeneity in accurately predicting even average population properties. Moreover, we find that unequal partitioning at cell division and sharp division rates shrink the region of the parameter space where the population exhibits bistable behavior, a characteristic feature of networks with positive feedback architecture. In addition, intrinsic noise at the single-cell level due to slow operator fluctuations and small numbers of molecules further contributes toward the shrinkage of the bistability regime at the cell population level. Finally, the effect of intrinsic noise at the cell population level was found to be markedly different than at the single-cell level, emphasizing the importance of simulating entire cell populations and not just individual cells to understand the complex interplay between single-cell genetic architecture and behavior at the cell population level.

FIGURE 1

Effect of rate of operator fluctuations (K) on the region of bistability at the single-cell level (δ = 1 and y* = 1000). (Solid lines) Single-cell deterministic model (steady state of Eq. 12). (Symbols) Single-cell stochastic model. (a) K = 200,000, (b) K = 2,000, and (c) K = 50.

FIGURE 2

Effect of number of molecules (y*) on the region of bistability at the single-cell level (δ = 1 and K = 200,000). (Solid lines) Single-cell deterministic model (steady state of Eq. 12). (Symbols) Single-cell stochastic model. (a) y* = 1,000, (b) y* = 50, and (c) y* = 20.

FIGURE 3

Effect of partitioning asymmetry (f) on average gene expression at the cell-population level as a function of dimensionless parameter ρ (m = 2, π = 0.03, δ = 0.05). (Dashed line) Continuum model. (Solid line, open triangles) f = 0.5. (Dashed line, solid squares) f = 0.4. (Solid line, open squares) f = 0.3. (Dashed line, solid circles) f = 0.2. (Solid line, open circles) f = 0.1.

FIGURE 4

Effect of sharpness of division rate (m) on average gene expression at the cell-population level as a function of dimensionless parameter ρ (f = 0.3, π = 0.03, δ = 0.05). (Dashed line) Continuum model. (Solid line, open triangles) m = 8.(Dashed line, solid squares) m = 5. (Solid line, open squares) m = 3. (Dashed line, solid circles) m = 2. (Solid line, open circles) m = 1.

FIGURE 5

Three time-invariant number density functions, normalized around the average expression level, coexisting in the bistable regime of the parameter space (m = 2, f = 0.3, π = 0.03, δ = 0.05, and ρ = 0.1). (Solid line, open circles) Stable steady state corresponding to highest average expression level. (Dashed line, solid circles) Unstable steady state corresponding to intermediate average expression level. (Solid line, open squares) Stable steady state corresponding to lowest average expression level.

FIGURE 6

Effect of partitioning asymmetry (f) on the shape of the normalized around the average expression level, time-invariant number density function in the monostable regime of the parameter space (m = 2, π = 0.03, δ = 0.05, and ρ = 0.03(Solid line, open circles) f = 0.1. (Dashed line, solid circles) f = 0.2. (Solid line, open squares) f = 0.3. (Dashed line, solid squares) f = 0.4. (Solid line, open triangles) f = 0.5.

FIGURE 7

Schematic of the SVNMC algorithm that accounts for both intrinsic and extrinsic sources of cell population heterogeneity. See text for detailed description.

FIGURE 8

Validation of the SVNMC algorithm: comparison of SVNMC predictions (dashed lines) with DCPB model predictions (solid lines) for very low intrinsic noise (K = 50,000, y* = 100,000) and for m = 2, f = 0.2, π = 0.03, δ = 0.05, and ρ = 0.02. (a) τ = 0, (b) τ = 0.195, (c) τ = 0.405, (d) τ = 0.595, (e) τ = 1.005, (f) τ = 1.405, (g) τ = 1.995, (h) τ = 2.995, and (i) τ = 5.

FIGURE 9

Effect of significant intrinsic noise (K = 500, y* = 50) on number density function dynamics for m = 2, f = 0.3, π = 0.03, δ = 0.05, and ρ = 0.07. (Solid lines) Predictions of the DCPB model neglecting intrinsic noise effects. (Dashed lines) Predictions of SVNMC algorithm. (a) τ = 0, (b) τ = 0.2, (c) τ = 0.6, (d) τ = 1, (e) τ = 1.5, (f) τ = 2, (g) τ = 5, (h) τ = 10, and (i) τ = 20.

FIGURE 10

Decomposing the effects of intrinsic and extrinsic heterogeneity by comparing the predictions of i), the SVNMC model (dashed line), ii), the corresponding DCPB model (solid line), and iii), the corresponding continuum model (solid line, open circles) for the average expression level. Common parameter values in all three models: π = 0.03, δ = 0.05, and ρ = 0.07. Common parameter values for DCPB and SVNMC models: m = 2, f = 0.3. Parameter values appearing only in SVNMC model: K = 500, y* = 50. (a) Average expression levels as predicted by the three models. (b) Coefficients of variation for the number density function as predicted by the SVNMC and DCPB models.

FIGURE 11

Asymptotic average expression level predicted by the DCPB (solid line) and SVNMC (symbols) models as a function of dimensionless parameter ρ for π = 0.03, δ = 0.05, m = 2, and f = 0.3. Intrinsic noise parameters: K = 500, y* = 50. In the case of SVNMC, the results of three simulations are plotted for each value of ρ.

FIGURE 12

Loss of bistability at the population level due to intrinsic noise. Dynamics of average expression level (a) and coefficient of variation of the number density function (b) as predicted by the DCPB (solid lines) and SVNMC (dashed lines) models for two different initial conditions: i), 〈x〉_o = 0.1, σ_o = 0.025; and ii), 〈x〉_o = 0.25, σ_o = 0.05 (open symbols). (a) Average expression level. Parameter values for both models: π = 0.03, δ = 0.05, ρ = 0.1, m = 2, and f = 0.3. Intrinsic noise parameters, K = 500, y* = 50.