Ballooning dispersal in arthropod taxa: conditions at take-off
- PMID: 17389214
- PMCID: PMC2464704
- DOI: 10.1098/rsbl.2007.0109
Ballooning dispersal in arthropod taxa: conditions at take-off
Abstract
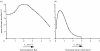
We have solved a long-standing and seemingly paradoxical set of questions that relate to the conditions which govern spider ballooning. We show that observations of spider ballooning excursions are best explained by meteorological conditions which maximize dispersal. Dispersal is predicted to be most effective in terms of distance when the stability of the atmosphere is non-ideally convective and is less effective during purely convective or neutrally stable conditions. Ballooners are most likely to travel a few hundred metres, but dispersal distances of several hundred kilometres are possible.
Figures
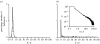
References
-
- Aylor D.E, Flesch T.K. Estimating spore release rates using a Lagrangian stochastic simulation model. J. Appl. Meteorol. 2001;40:1196–1208. doi:10.1175/1520-0450(2001)040<1196:ESRRUA>2.0.CO;2 - DOI
-
- Bell J.R, Bohan D.A, Shaw E.M, Weyman G.S. Ballooning dispersal using silk: world fauna, phylogenies, genetics and models. Bull. Entomol. Res. 2005;95:69–114. doi:10.1079/BER2004350 - DOI - PubMed
-
- Brown J.K.M, Hovmoller M.S. Aerial dispersal of pathogens on the global and continental scales and its impact on plant disease. Science. 2002;297:537–541. doi:10.1126/science.1072678 - DOI - PubMed
-
- Burrows F.M. The aerial motion of seeds, fruits, spores and pollen. In: Murray D.R, editor. Seed dispersal. Academic Press; Sydney, Australia: 1986. pp. 1–47.
-
- Businger J.A. A note on the Businger–Dyer profiles. Bound.-Lay. Meteorol. 1988;42:145–151. doi:10.1007/BF00119880 - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
