Coarse-grained analysis of stochasticity-induced switching between collective motion states
- PMID: 17389400
- PMCID: PMC1851594
- DOI: 10.1073/pnas.0608270104
Coarse-grained analysis of stochasticity-induced switching between collective motion states
Abstract
A single animal group can display different types of collective motion at different times. For a one-dimensional individual-based model of self-organizing group formation, we show that repeated switching between distinct ordered collective states can occur entirely because of stochastic effects. We introduce a framework for the coarse-grained, computer-assisted analysis of such stochasticity-induced switching in animal groups. This involves the characterization of the behavior of the system with a single dynamically meaningful "coarse observable" whose dynamics are described by an effective Fokker-Planck equation. A "lifting" procedure is presented, which enables efficient estimation of the necessary macroscopic quantities for this description through short bursts of appropriately initialized computations. This leads to the construction of an effective potential, which is used to locate metastable collective states, and their parametric dependence, as well as estimate mean switching times.
Conflict of interest statement
The authors declare no conflict of interest.
Figures

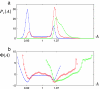


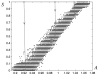
Similar articles
-
Gene regulatory networks: a coarse-grained, equation-free approach to multiscale computation.J Chem Phys. 2006 Feb 28;124(8):084106. doi: 10.1063/1.2149854. J Chem Phys. 2006. PMID: 16512707
-
Making noise: emergent stochasticity in collective motion.J Theor Biol. 2010 Dec 7;267(3):292-9. doi: 10.1016/j.jtbi.2010.08.034. Epub 2010 Sep 8. J Theor Biol. 2010. PMID: 20816990
-
Inherent noise can facilitate coherence in collective swarm motion.Proc Natl Acad Sci U S A. 2009 Apr 7;106(14):5464-9. doi: 10.1073/pnas.0811195106. Epub 2009 Mar 31. Proc Natl Acad Sci U S A. 2009. PMID: 19336580 Free PMC article.
-
Locust Collective Motion and Its Modeling.PLoS Comput Biol. 2015 Dec 10;11(12):e1004522. doi: 10.1371/journal.pcbi.1004522. eCollection 2015 Dec. PLoS Comput Biol. 2015. PMID: 26656851 Free PMC article. Review.
-
Compatible quantum theory.Rep Prog Phys. 2014 Sep;77(9):092001. doi: 10.1088/0034-4885/77/9/092001. Epub 2014 Aug 22. Rep Prog Phys. 2014. PMID: 25146940 Review.
Cited by
-
Self-organization across scales: from molecules to organisms.Philos Trans R Soc Lond B Biol Sci. 2018 May 26;373(1747):20170113. doi: 10.1098/rstb.2017.0113. Philos Trans R Soc Lond B Biol Sci. 2018. PMID: 29632265 Free PMC article. Review.
-
Direction-dependent interaction rules enrich pattern formation in an individual-based model of collective behavior.PLoS One. 2018 Jun 14;13(6):e0198550. doi: 10.1371/journal.pone.0198550. eCollection 2018. PLoS One. 2018. PMID: 29902189 Free PMC article.
-
How the spatial position of individuals affects their influence on swarms: a numerical comparison of two popular swarm dynamics models.PLoS One. 2013;8(3):e58525. doi: 10.1371/journal.pone.0058525. Epub 2013 Mar 21. PLoS One. 2013. PMID: 23555585 Free PMC article.
-
Multiscale cancer modeling.Annu Rev Biomed Eng. 2011 Aug 15;13:127-55. doi: 10.1146/annurev-bioeng-071910-124729. Annu Rev Biomed Eng. 2011. PMID: 21529163 Free PMC article. Review.
-
Social conformity and propagation of information in collective U-turns of fish schools.Proc Biol Sci. 2018 Apr 25;285(1877):20180251. doi: 10.1098/rspb.2018.0251. Proc Biol Sci. 2018. PMID: 29695447 Free PMC article.
References
-
- Camazine S, Deneubourg J-L, Franks NR, Sneyd J, Theraula G, Bonabeau E. Self-Organization in Biological Systems. Princeton: Princeton Univ Press; 2001.
-
- Parrish JK, Edelstein-Keshet L. Science. 1999;284:99–101. - PubMed
-
- Koltes KH. Mar Biol. 1984;78:113–122.
-
- Aoki I. Bull Jap Soc Fish. 1982;48:1081–1088.
-
- Warburton K, Lazarus J. J Theor Biol. 1991;150:473–488. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

