Backup without redundancy: genetic interactions reveal the cost of duplicate gene loss
- PMID: 17389874
- PMCID: PMC1847942
- DOI: 10.1038/msb4100127
Backup without redundancy: genetic interactions reveal the cost of duplicate gene loss
Abstract
Many genes can be deleted with little phenotypic consequences. By what mechanism and to what extent the presence of duplicate genes in the genome contributes to this robustness against deletions has been the subject of considerable interest. Here, we exploit the availability of high-density genetic interaction maps to provide direct support for the role of backup compensation, where functionally overlapping duplicates cover for the loss of their paralog. However, we find that the overall contribution of duplicates to robustness against null mutations is low ( approximately 25%). The ability to directly identify buffering paralogs allowed us to further study their properties, and how they differ from non-buffering duplicates. Using environmental sensitivity profiles as well as quantitative genetic interaction spectra as high-resolution phenotypes, we establish that even duplicate pairs with compensation capacity exhibit rich and typically non-overlapping deletion phenotypes, and are thus unable to comprehensively cover against loss of their paralog. Our findings reconcile the fact that duplicates can compensate for each other's loss under a limited number of conditions with the evolutionary instability of genes whose loss is not associated with a phenotypic penalty.
Figures
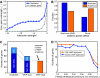
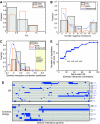
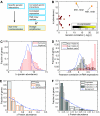
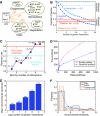
Comment in
-
Genetic interactions in yeast: is robustness going bust?Mol Syst Biol. 2007;3:97. doi: 10.1038/msb4100146. Epub 2007 Mar 27. Mol Syst Biol. 2007. PMID: 17389877 Free PMC article. No abstract available.
References
-
- Brookfield J (1992) Can genes be truly redundant? Curr Biol 2: 553–554 - PubMed
-
- Collins SR, Miller KM, Maas NL, Roguev A, Fillingham J, Chu CS, Schuldiner M, Gebbia M, Recht J, Shales M, Ding H, Xu H, Han J, Ingvarsdottir K, Cheng B, Andrews B, Berger SL, Hieter P, Zhang Z, Brown GW, Ingles J, Boone C, Emili A, Allis CD, Toczyski DP, Weissman JS, Greenblatt JF, Krogan NJ (2007) Functional dissection of yeast chromosome biology complexes using a genetic interaction map. Nature (in press) - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

