Evolution of coadaptation in a subdivided population
- PMID: 17409093
- PMCID: PMC1893032
- DOI: 10.1534/genetics.106.063636
Evolution of coadaptation in a subdivided population
Abstract
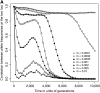
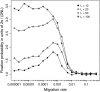
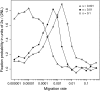
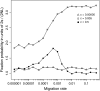
The interplay between population subdivision and epistasis is investigated by studying the fixation probability of a coadapted haplotype in a subdivided population. Analytical and simulation models are developed to study the evolutionary fate of two conditionally neutral mutations that interact epistatically to enhance fitness. We find that the fixation probability of a coadapted haplotype shows a marked increase when the population is genetically subdivided and subpopulations are loosely connected by migration. Moderate migration and isolation allow the propagation of the mutant alleles across subpopulations, while at the same time preserving the favorable allelic combination established within each subpopulation. Together they create the condition most favorable for the ultimate fixation of the coadapted haplotype. On the basis of the analytical and simulation results, we discuss the fundamental role of population subdivision and restricted gene flow in promoting the evolution of functionally integrated systems, with some implications for the shifting-balance theory of evolution.
Figures




Similar articles
-
Coalescent under the evolution of coadaptation.Mol Ecol. 2009 Dec;18(24):5018-29. doi: 10.1111/j.1365-294X.2009.04424.x. Epub 2009 Nov 11. Mol Ecol. 2009. PMID: 19912539
-
Evolution of coadaptation in a two-locus epistatic system.Evolution. 2005 Nov;59(11):2324-32. Evolution. 2005. PMID: 16396173
-
Population structure, fitness surfaces, and linkage in the shifting balance process.Genet Res. 1995 Aug;66(1):85-92. doi: 10.1017/s0016672300034418. Genet Res. 1995. PMID: 8575671
-
Perspective: Sign epistasis and genetic constraint on evolutionary trajectories.Evolution. 2005 Jun;59(6):1165-74. Evolution. 2005. PMID: 16050094 Review.
-
The conversion of variance and the evolutionary potential of restricted recombination.Heredity (Edinb). 2006 Feb;96(2):111-21. doi: 10.1038/sj.hdy.6800772. Heredity (Edinb). 2006. PMID: 16333302 Review.
Cited by
-
Simulation of DNA sequence evolution under models of recent directional selection.Brief Bioinform. 2009 Jan;10(1):84-96. doi: 10.1093/bib/bbn048. Epub 2008 Dec 24. Brief Bioinform. 2009. PMID: 19109303 Free PMC article.
-
A linkage disequilibrium-based statistical test for Genome-Wide Epistatic Selection Scans in structured populations.Heredity (Edinb). 2021 Jan;126(1):77-91. doi: 10.1038/s41437-020-0349-1. Epub 2020 Jul 30. Heredity (Edinb). 2021. PMID: 32728044 Free PMC article.
-
The dynamics of mutations associated with anti-malarial drug resistance in Plasmodium falciparum.Trends Parasitol. 2009 Dec;25(12):557-63. doi: 10.1016/j.pt.2009.09.008. Epub 2009 Oct 26. Trends Parasitol. 2009. PMID: 19864183 Free PMC article. Review.
-
Plasmodium falciparum produce lower infection intensities in local versus foreign Anopheles gambiae populations.PLoS One. 2012;7(1):e30849. doi: 10.1371/journal.pone.0030849. Epub 2012 Jan 26. PLoS One. 2012. PMID: 22292059 Free PMC article.
-
Screening for epistatic selection signatures: A simulation study.Sci Rep. 2019 Jan 31;9(1):1026. doi: 10.1038/s41598-019-38689-2. Sci Rep. 2019. PMID: 30705409 Free PMC article.
References
-
- Barton, N. H., 1993. The probability of fixation of a favoured allele in a subdivided population. Genet. Res. 62: 149–157.
-
- Briggs, C. J., and M. F. Hoopes, 2004. Stabilizing effects in spatial parasitoid-host and predator-prey models: a review. Theor. Popul. Biol. 65: 299–315. - PubMed
-
- Chave, J., H. C. Muller-Landau and S. A. Levin, 2002. Comparing classical community models: theoretical consequences for patterns of diversity. Am. Nat. 159: 1–23. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

