Revision of the theory of tracer transport and the convolution model of dynamic contrast enhanced magnetic resonance imaging

Abstract

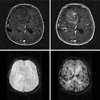
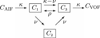
Counterexamples are used to motivate the revision of the established theory of tracer transport. Then dynamic contrast enhanced magnetic resonance imaging in particular is conceptualized in terms of a fully distributed convection-diffusion model from which a widely used convolution model is derived using, alternatively, compartmental discretizations or semigroup theory. On this basis, applications and limitations of the convolution model are identified. For instance, it is proved that perfusion and tissue exchange states cannot be identified on the basis of a single convolution equation alone. Yet under certain assumptions, particularly that flux is purely convective at the boundary of a tissue region, physiological parameters such as mean transit time, effective volume fraction, and volumetric flow rate per unit tissue volume can be deduced from the kernel.

Fig. 1

Compartment networks with a purely convective exchange shown on the left, and b convective and diffusive exchange shown on the right. The parameters in (3.2) may be chosen so that the respective residue functions are identical

Fig. 2

Magnetic resonance images taken from a series of images measured during the injection of a Gadolinium-DTPA based contrast agent. From left to right the images were taken, respectively, before and after the appearance of the contrast agent. The first row shows T₁-weighted images while the second row shows $T_2^{*}$-weighted images

Fig. 3

Simple geometry for the solution of the convection diffusion equation (3.1)

Fig. 4

A chain of compartments connecting the arterial input with the venous output, where the constants k_i are purely convective and the constants k_ij are purely diffusive

Fig. 5

A compartment network implicitly incorporating arbitrarily oriented diffusion at convective pathway branch points