Analysis of epistatic interactions and fitness landscapes using a new geometric approach
- PMID: 17433106
- PMCID: PMC1865543
- DOI: 10.1186/1471-2148-7-60
Analysis of epistatic interactions and fitness landscapes using a new geometric approach
Abstract
Background: Understanding interactions between mutations and how they affect fitness is a central problem in evolutionary biology that bears on such fundamental issues as the structure of fitness landscapes and the evolution of sex. To date, analyses of fitness landscapes have focused either on the overall directional curvature of the fitness landscape or on the distribution of pairwise interactions. In this paper, we propose and employ a new mathematical approach that allows a more complete description of multi-way interactions and provides new insights into the structure of fitness landscapes.
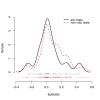
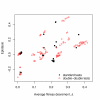
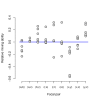
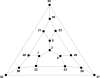
Results: We apply the mathematical theory of gene interactions developed by Beerenwinkel et al. to a fitness landscape for Escherichia coli obtained by Elena and Lenski. The genotypes were constructed by introducing nine mutations into a wild-type strain and constructing a restricted set of 27 double mutants. Despite the absence of mutants higher than second order, our analysis of this genotypic space points to previously unappreciated gene interactions, in addition to the standard pairwise epistasis. Our analysis confirms Elena and Lenski's inference that the fitness landscape is complex, so that an overall measure of curvature obscures a diversity of interaction types. We also demonstrate that some mutations contribute disproportionately to this complexity. In particular, some mutations are systematically better than others at mixing with other mutations. We also find a strong correlation between epistasis and the average fitness loss caused by deleterious mutations. In particular, the epistatic deviations from multiplicative expectations tend toward more positive values in the context of more deleterious mutations, emphasizing that pairwise epistasis is a local property of the fitness landscape. Finally, we determine the geometry of the fitness landscape, which reflects many of these biologically interesting features.
Conclusion: A full description of complex fitness landscapes requires more information than the average curvature or the distribution of independent pairwise interactions. We have proposed a mathematical approach that, in principle, allows a complete description and, in practice, can suggest new insights into the structure of real fitness landscapes. Our analysis emphasizes the value of non-independent genotypes for these inferences.
Figures
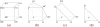
References
-
- Beerenwinkel N, Pachter L, Sturmfels B. Epistasis and shapes of fitness landscapes. Statistica Sinica.
-
- Wright S. The roles of mutation, inbreeding, crossbreeding, and selection in evolution. Proc Sixth Intl Cong Genetics. 1932;1:356–366.
-
- Fisher RA. The Genetical Theory of Natural Selection. Oxford University Press; 1930. - PubMed
-
- Simpson GG. The Major Features of Evolution. Columbia University Press; 1953.

