Bayesian shrinkage analysis of quantitative trait Loci for dynamic traits

Abstract

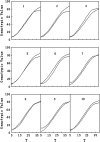
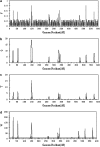
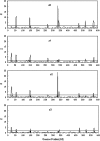
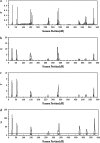
Many quantitative traits are measured repeatedly during the life of an organism. Such traits are called dynamic traits. The pattern of the changes of a dynamic trait is called the growth trajectory. Studying the growth trajectory may enhance our understanding of the genetic architecture of the growth trajectory. Recently, we developed an interval-mapping procedure to map QTL for dynamic traits under the maximum-likelihood framework. We fit the growth trajectory by Legendre polynomials. The method intended to map one QTL at a time and the entire QTL analysis involved scanning the entire genome by fitting multiple single-QTL models. In this study, we propose a Bayesian shrinkage analysis for estimating and mapping multiple QTL in a single model. The method is a combination between the shrinkage mapping for individual quantitative traits and the Legendre polynomial analysis for dynamic traits. The multiple-QTL model is implemented in two ways: (1) a fixed-interval approach where a QTL is placed in each marker interval and (2) a moving-interval approach where the position of a QTL can be searched in a range that covers many marker intervals. Simulation study shows that the Bayesian shrinkage method generates much better signals for QTL than the interval-mapping approach. We propose several alternative methods to present the results of the Bayesian shrinkage analysis. In particular, we found that the Wald test-statistic profile can serve as a mechanism to test the significance of a putative QTL.

Figure 1.—

Illustration of the problem with dense marker map and the sketch of a proposed solution. The line at the top shows 7 markers () with intermediate density and 6 QTL (), one in each marker interval. The Bayesian shrinkage method works well without modification. The line in the middle shows the problem of too many correlated variables if the marker density is extremely high. There are 18 markers () and 17 QTL (), one in each marker interval. The line at the bottom shows the solution where we can define a QTL interval covering several markers and assign 1 QTL to each so defined interval. Here, there are 18 markers () but only 5 QTL () and each QTL interval covers several markers.

Figure 2.—

Illustration of the moving-interval search algorithm for QTL on a chromosome with saturated markers. The first line shows the marker map and the initial positions of five QTL. The second line shows that the position of can move between and . Once the position of is sampled, can move between and (third line). The position of each QTL moves sequentially conditional on the positions of other QTL until positions of all QTL have been updated, which completes one cycle of the sampling (lines 4–6). The line at the bottom shows the new positions of the five QTL after one cycle of the iteration.

Figure 3.—

The trajectories of genotypic effects for 9 of the 10 simulated QTL (the fourth QTL effects are not included in the plots). The genotypic value for one genotype is and the value for the alternative genotype is , where t is the standardized time point and T is the original time point ranging from 5 to 40.

Figure 4.—

Profiles of QTL parameters drawn from the fixed-interval analysis: (a) QTL intensity profile , (b) quadratic effect profile , (c) weighted quadratic effect profile , and (d) Wald test statistic profile . The horizontal reference line on the W plot (plot d) is the critical value for the Wald test statistic (). The true location of each simulated QTL is indicated by a solid needle on the horizontal axis.

Figure 5.—

The Z-test-statistic profile for each of the four components of the QTL effect obtained from the fixed-interval analysis, where is the component for order k of the polynomial. The reference line on each plot is the critical value for the Z-test ().

Figure 6.—

Estimated growth trajectories for the effects of the nine detected QTL with the fixed-interval approach, where and are the trajectories of the two alternative genotypes for each QTL.

Figure 7.—

The likelihood-ratio (LR) test-statistic profile for the simulated data generated by the dynamic trait interval-mapping program. The horizontal line indicates the empirical critical value at obtained from 500 permuted samples. The true location of each simulated QTL is indicated by a solid needle on the horizontal axis.

Figure 8.—

Profiles of QTL parameters drawn from the moving-interval analysis: (a) QTL intensity profile , (b) quadratic effect profile , (c) weighted quadratic effect profile , and (d) Wald test-statistic profile . The horizontal reference line on the W plot (plot d) is the critical value for the Wald test statistic ().

Figure 9.—

The Z-test-statistic profile for each of the four components of the QTL effect from the moving-interval analysis, where is the component for order k of the polynomial. The reference line on each plot is the critical value for the Z-test ().

Figure 10.—

The test-statistic profiles for QTL mapping from the rice data analysis: (a) The Wald test-statistic (W) profile generated by the Bayesian shrinkage method; (b) the likelihood-ratio (LR) test-statistic profile drawn from the maximum-likelihood interval-mapping analysis. The horizontal reference line in the W plot (top) is the critical value () for the significance test. The horizontal reference line in the LR plot (bottom) is the empirical critical value at a type I error rate of for the LR test statistic generated from permutation tests. The genome consists of 12 chromosomes that are separated by the vertical dotted lines. The 12 chromosomes are drawn in scales proportional to their lengths. Positions of the markers are indicated by the ticks on the horizontal axis.