Using the wild bootstrap to quantify uncertainty in diffusion tensor imaging
- PMID: 17455199
- PMCID: PMC6870960
- DOI: 10.1002/hbm.20395
Using the wild bootstrap to quantify uncertainty in diffusion tensor imaging
Abstract
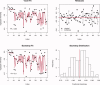
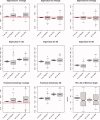
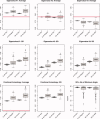
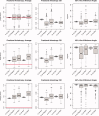
Estimation of noise-induced variability in diffusion tensor imaging (DTI) is needed to objectively follow disease progression in therapeutic monitoring and to provide consistent readouts of pathophysiology. The noise variability of nonlinear quantities of the diffusion tensor (e.g., fractional anisotropy, fiber orientation, etc.) have been quantified using the bootstrap, in which the data are resampled from the experimental averages, yet this approach is only applicable to DTI scans that contain multiple averages from the same sampling direction. It has been shown that DTI acquisitions with a modest to large number of directions, in which each direction is only sampled once, outperform the multiple averages approach. These acquisitions resist the traditional (regular) bootstrap analysis though. In contrast to the regular bootstrap, the wild bootstrap method can be applied to such protocols in which there is only one observation per direction. Here, we compare and contrast the wild bootstrap with the regular bootstrap using Monte Carlo numerical simulations for a number of diffusion scenarios. The regular and wild bootstrap methods are applied to human DTI data and empirical distributions are obtained for fractional anisotropy and the diffusion tensor eigensystem. Spatial maps of the estimated variability in the diffusion tensor principal eigenvector are provided. The wild bootstrap method can provide empirical distributions for tensor-derived quantities, such as fractional anisotropy and principal eigenvector direction, even when the exact distributions are not easily derived.
Figures



References
-
- Anderson AW( 2001): Theoretical analysis of the effects of noise on diffusion tensor imaging. Magn Reson Med 46: 1174–1188. - PubMed
-
- Basford KE, Greenway DR, McLachlan GJ, Peel D( 1997): Standard errors of fitted means under normal mixture models. Comput Stat 12: 1–17.
-
- Basser PJ, Mattiello J, LeBihan D( 1994): Estimation of the effective self‐diffusion tensor from the NMR spin echo. J Magn Reson 103: 247–254. - PubMed
-
- Batchelor PG, Atkinson D, Hill DLG, Calamante F, Connelly A( 2003): Anisotropic noise propagation in diffusion tensor MRI sampling schemes. Magn Reson Med 49: 1143–1151. - PubMed
-
- Behrens TEJ, Woolrich MW, Jenkinson M, Johansen‐Berg H, Nunes RG, Clare S, Matthews PM, Brady JM, Smith SM( 2003): Characterization and propogation of uncertainty in diffusion‐weighted MR imaging. Magn Reson Med 50: 1077–1088. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

