Structure and tie strengths in mobile communication networks
- PMID: 17456605
- PMCID: PMC1863470
- DOI: 10.1073/pnas.0610245104
Structure and tie strengths in mobile communication networks
Abstract
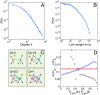
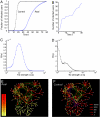
Electronic databases, from phone to e-mails logs, currently provide detailed records of human communication patterns, offering novel avenues to map and explore the structure of social and communication networks. Here we examine the communication patterns of millions of mobile phone users, allowing us to simultaneously study the local and the global structure of a society-wide communication network. We observe a coupling between interaction strengths and the network's local structure, with the counterintuitive consequence that social networks are robust to the removal of the strong ties but fall apart after a phase transition if the weak ties are removed. We show that this coupling significantly slows the diffusion process, resulting in dynamic trapping of information in communities and find that, when it comes to information diffusion, weak and strong ties are both simultaneously ineffective.
Conflict of interest statement
Conflict of interest statement: A.L.B. served as a paid consultant for the phone company that provided the phone data.
Figures


References
-
- Ebel H, Mielsch L-I, Bornholdt S. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Top. 2002;66:35103. - PubMed
-
- Dodds PS, Muhamad R, Watts DJ. Science. 2003;301:827–829. - PubMed
-
- Aiello W, Chung F, Lu L. Proceedings of the 32nd ACM Symposium on the Theory of Computing; New York: Assoc Comput Machinery; 2000. pp. 171–180.
-
- Wasserman S, Faust K. Social Network Analysis: Methods and Applications. Cambridge: Cambridge Univ Press; 1994.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

