The oesophageal zero-stress state and mucosal folding from a GIOME perspective
- PMID: 17457964
- PMCID: PMC4146917
- DOI: 10.3748/wjg.v13.i9.1347
The oesophageal zero-stress state and mucosal folding from a GIOME perspective
Abstract
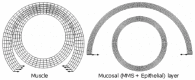
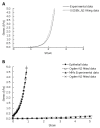
The oesophagus is a cylindrical organ with a collapsed lumen and mucosal folds. The mucosal folding may serve to advance the function of the oesophagus, i.e. the folds have a major influence on the flow of air and bolus through the oesophagus. Experimental studies have demonstrated oesophageal mucosal folds in the no-load state. This indicates that mucosal buckling must be considered in the analysis of the mechanical reference state since the material stiffness drops dramatically after tissue collapse. Most previous work on the oesophageal zero-stress state and mucosal folding has been experimental. However, numerical analysis offers a promising alternative approach, with the additional ability to predict the mucosal buckling behaviour and to calculate the regional stress and strain in complex structures. A numerical model used for describing the mechanical behaviour of the mucosal-folded, three-layered, two-dimensional oesophageal model is reviewed. GIOME models can be used in the future to predict the tissue function physiologically and pathologically.
Figures
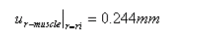
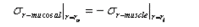

Similar articles
-
Regional distribution of axial strain and circumferential residual strain in the layered rabbit oesophagus.J Biomech. 2001 Feb;34(2):225-33. doi: 10.1016/s0021-9290(00)00176-7. J Biomech. 2001. PMID: 11165287
-
Stress distribution in the layered wall of the rat oesophagus.Med Eng Phys. 2003 Nov;25(9):731-8. doi: 10.1016/s1350-4533(03)00122-x. Med Eng Phys. 2003. PMID: 14519345
-
Growth and surface folding of esophageal mucosa: a biomechanical model.J Biomech. 2011 Jan 4;44(1):182-8. doi: 10.1016/j.jbiomech.2010.09.007. Epub 2010 Sep 28. J Biomech. 2011. PMID: 20880530
-
Review article: oesophageal mucosal resistance.Aliment Pharmacol Ther. 1998 Mar;12(3):191-7. doi: 10.1046/j.1365-2036.1998.00308.x. Aliment Pharmacol Ther. 1998. PMID: 9570252 Review.
-
Three-dimensional surface model analysis in the gastrointestinal tract.World J Gastroenterol. 2006 May 14;12(18):2870-5. doi: 10.3748/wjg.v12.i18.2870. World J Gastroenterol. 2006. PMID: 16718811 Free PMC article. Review.
Cited by
-
Gastrointestinal tract modelling in health and disease.World J Gastroenterol. 2009 Jan 14;15(2):169-76. doi: 10.3748/wjg.15.169. World J Gastroenterol. 2009. PMID: 19132766 Free PMC article. Review.
-
Artery buckling: new phenotypes, models, and applications.Ann Biomed Eng. 2013 Jul;41(7):1399-410. doi: 10.1007/s10439-012-0707-0. Epub 2012 Nov 29. Ann Biomed Eng. 2013. PMID: 23192265 Free PMC article. Review.
-
On the mechanics of continua with boundary energies and growing surfaces.J Mech Phys Solids. 2013 Jun 1;61(6):1446-1463. doi: 10.1016/j.jmps.2013.01.007. J Mech Phys Solids. 2013. PMID: 23606760 Free PMC article.
-
On the mechanics of thin films and growing surfaces.Math Mech Solids. 2013 Aug;18(6):561-575. doi: 10.1177/1081286513485776. Epub 2013 May 24. Math Mech Solids. 2013. PMID: 36466793 Free PMC article.
-
Computational simulations of the helical buckling behavior of blood vessels.Int J Numer Method Biomed Eng. 2019 Dec;35(12):e3277. doi: 10.1002/cnm.3277. Epub 2019 Nov 27. Int J Numer Method Biomed Eng. 2019. PMID: 31680465 Free PMC article.
References
-
- Gregersen H, Kassab GS, Fung YC. The zero-stress state of the gastrointestinal tract: biomechanical and functional implications. Dig Dis Sci. 2000;45:2271–2281. - PubMed
-
- Gregersen H. Βiomechanics of the Gastrointestinal Tract. London: Springer; 2002. - PubMed
-
- Chuong CJ, Fung YC. On residual stresses in arteries. J Biomech Eng. 1986;108:189–192. - PubMed
-
- Fung YC. Biomechanics: Mechanical Properties of Living Tissues. New York: Springer-Verlag; 1993.
-
- Liao D, Zhao J, Fan Y, Gregersen H. Two-layered quasi-3D finite element model of the oesophagus. Med Eng Phys. 2004;26:535–543. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

