Finite element simulation of food transport through the esophageal body
- PMID: 17457965
- PMCID: PMC4146918
- DOI: 10.3748/wjg.v13.i9.1352
Finite element simulation of food transport through the esophageal body
Abstract
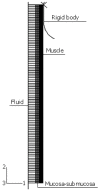
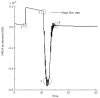
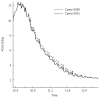
The peristaltic transport of swallowed material in the esophagus is a neuro-muscular function involving the nerve control, bolus-structure interaction, and structure-mechanics relationship of the tissue. In this study, a finite element model (FEM) was developed to simulate food transport through the esophagus. The FEM consists of three components, i.e., tissue, food bolus and peristaltic wave, as well as the interactions between them. The transport process was simulated as three stages, i.e., the filling of fluid, contraction of circular muscle and traveling of peristaltic wave. It was found that the maximal passive intraluminal pressure due to bolus expansion was in the range of 0.8-10 kPa and it increased with bolus volume and fluid viscosity. It was found that the highest normal and shear stresses were at the inner surface of muscle layer. In addition, the peak pressure required for the fluid flow was predicted to be 1-15 kPa at the bolus tail. The diseases of systemic sclerosis or osteogenesis imperfecta, with the remodeled microstructures and mechanical properties, might induce the malfunction of esophageal transport. In conclusion, the current simulation was demonstrated to be able to capture the main characteristics in the intraluminal pressure and bolus geometry as measured experimentally. Therefore, the finite element model established in this study could be used to further explore the mechanism of esophageal transport in various clinical applications.
Figures


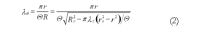



Similar articles
-
The mechanical advantage of local longitudinal shortening on peristaltic transport.J Biomech Eng. 2002 Feb;124(1):94-100. doi: 10.1115/1.1427700. J Biomech Eng. 2002. PMID: 11871611
-
Local longitudinal muscle shortening of the human esophagus from high-frequency ultrasonography.Am J Physiol Gastrointest Liver Physiol. 2001 Oct;281(4):G1022-33. doi: 10.1152/ajpgi.2001.281.4.G1022. Am J Physiol Gastrointest Liver Physiol. 2001. PMID: 11557523
-
Determinants of intrabolus pressure during esophageal peristaltic bolus transport.Am J Physiol. 1993 Mar;264(3 Pt 1):G407-13. doi: 10.1152/ajpgi.1993.264.3.G407. Am J Physiol. 1993. PMID: 8460696
-
Function of longitudinal vs circular muscle fibers in esophageal peristalsis, deduced with mathematical modeling.World J Gastroenterol. 2007 Mar 7;13(9):1335-46. doi: 10.3748/wjg.v13.i9.1335. World J Gastroenterol. 2007. PMID: 17457963 Free PMC article. Review.
-
Neuromuscular mechanisms of primary peristalsis.Am J Med. 1997 Nov 24;103(5A):40S-43S. doi: 10.1016/s0002-9343(97)00320-3. Am J Med. 1997. PMID: 9422621 Review.
Cited by
-
Free Tools and Strategies for the Generation of 3D Finite Element Meshes: Modeling of the Cardiac Structures.Int J Biomed Imaging. 2013;2013:540571. doi: 10.1155/2013/540571. Epub 2013 May 16. Int J Biomed Imaging. 2013. PMID: 23762031 Free PMC article.
-
Gastrointestinal tract modelling in health and disease.World J Gastroenterol. 2009 Jan 14;15(2):169-76. doi: 10.3748/wjg.15.169. World J Gastroenterol. 2009. PMID: 19132766 Free PMC article. Review.
-
Mechanics informed fluoroscopy of esophageal transport.Biomech Model Mechanobiol. 2021 Jun;20(3):925-940. doi: 10.1007/s10237-021-01420-0. Epub 2021 Mar 2. Biomech Model Mechanobiol. 2021. PMID: 33651206 Free PMC article.
-
Mechanical experimentation of the gastrointestinal tract: a systematic review.Biomech Model Mechanobiol. 2024 Feb;23(1):23-59. doi: 10.1007/s10237-023-01773-8. Epub 2023 Nov 8. Biomech Model Mechanobiol. 2024. PMID: 37935880 Free PMC article.
References
-
- Liao D, Fan Y, Zeng Y, Gregersen H. Stress distribution in the layered wall of the rat oesophagus. Med Eng Phys. 2003;25:731–738. - PubMed
-
- Liao D, Zhao J, Fan Y, Gregersen H. Two-layered quasi-3D finite element model of the oesophagus. Med Eng Phys. 2004;26:535–543. - PubMed
-
- Li M, Brasseur JG, Dodds WJ. Analyses of normal and abnormal esophageal transport using computer simulations. Am J Physiol. 1994;266:G525–G543. - PubMed
-
- Li M, Brasseur JG. Non-steady peristaltic transport in finite-length tubes. J Fluid Mech. 1993;248:129–151.
-
- Brasseur JG, Dodds WJ. Interpretation of intraluminal manometric measurements in terms of swallowing mechanics. Dysphagia. 1991;6:100–119. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

