On the mechanical behavior of the human biliary system
- PMID: 17457970
- PMCID: PMC4146923
- DOI: 10.3748/wjg.v13.i9.1384
On the mechanical behavior of the human biliary system
Abstract
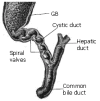
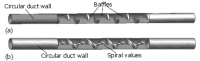
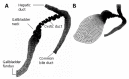
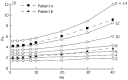
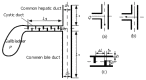
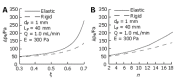
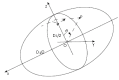
This paper reviews the progress made in understanding the mechanical behaviour of the biliary system. Gallstones and diseases of the biliary tract affect more than 10% of the adult population. The complications of gallstones, i.e. acute pancreatitis and obstructive jandice, can be lethal, and patients with acalculous gallbladder pain often pose diagnostic difficulties and undergo repeated ultrasound scans and oral cholecystograms. Moreover, surgery to remove the gallbladder in these patients, in an attempt to relieve the symptoms, gives variable results. Extensive research has been carried out to understand the physiological and pathological functions of the biliary system, but the mechanism of the pathogenesis of gallstones and pain production still remain poorly understood. It is believed that the mechanical factors play an essential role in the mechanisms of the gallstone formation and biliary diseases. However, despite the extensive literature in clinical studies, only limited work has been carried out to study the biliary system from the mechanical point of view. In this paper, we discuss the state of art knowledge of the fluid dynamics of bile flow in the biliary tract, the solid mechanics of the gallbladder and bile ducts, recent mathematical and numerical modelling of the system, and finally the future challenges in the area.
Figures
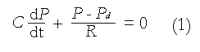
Similar articles
-
Gallbladder dyskinesia in acalculous biliary colic.Rev Esp Enferm Dig. 1996 Nov;88(11):770-9. Rev Esp Enferm Dig. 1996. PMID: 9004783 English, Spanish.
-
Cholesterol gallstone disease: focusing on the role of gallbladder.Lab Invest. 2015 Feb;95(2):124-31. doi: 10.1038/labinvest.2014.140. Epub 2014 Dec 15. Lab Invest. 2015. PMID: 25502177 Review.
-
Gallstones.Nat Rev Dis Primers. 2016 Apr 28;2:16024. doi: 10.1038/nrdp.2016.24. Nat Rev Dis Primers. 2016. PMID: 27121416 Review.
-
Introduction to the biliary tract, the gallbladder, and gallstones.Microsc Res Tech. 1997 Sep 15;38(6):547-51. doi: 10.1002/(SICI)1097-0029(19970915)38:6<547::AID-JEMT1>3.0.CO;2-C. Microsc Res Tech. 1997. PMID: 9330345 Review.
-
Small gallstones, preserved gallbladder motility, and fast crystallization are associated with pancreatitis.Hepatology. 2005 Apr;41(4):738-46. doi: 10.1002/hep.20616. Hepatology. 2005. PMID: 15793851
Cited by
-
Wet-tip versus dry-tip regimes of osmotically driven fluid flow.Sci Rep. 2019 Mar 14;9(1):4528. doi: 10.1038/s41598-019-40853-7. Sci Rep. 2019. PMID: 30872654 Free PMC article.
-
A Predictive 3D Multi-Scale Model of Biliary Fluid Dynamics in the Liver Lobule.Cell Syst. 2017 Mar 22;4(3):277-290.e9. doi: 10.1016/j.cels.2017.02.008. Epub 2017 Mar 18. Cell Syst. 2017. PMID: 28330614 Free PMC article.
-
Acute Cholecystitis Presenting With Septic Shock as the First Presentation in an Elderly Patient.Cureus. 2022 Jan 6;14(1):e20981. doi: 10.7759/cureus.20981. eCollection 2022 Jan. Cureus. 2022. PMID: 35004094 Free PMC article.
-
Versatile application of fast green FCF as a visible cholangiogram in adult mice to medium-sized mammals.Sci Rep. 2025 Jan 16;15(1):1960. doi: 10.1038/s41598-024-84355-7. Sci Rep. 2025. PMID: 39821095 Free PMC article.
-
Classification of anatomical morphology of cystic duct and its association with gallstone.World J Gastrointest Surg. 2024 Feb 27;16(2):307-317. doi: 10.4240/wjgs.v16.i2.307. World J Gastrointest Surg. 2024. PMID: 38463380 Free PMC article.
References
-
- Sandor J, Sandor A, Zaborszky A, Megyaszai S, Benedek G, Szeberin Z. Why laparoscopic cholecystectomy today? Surg Today. 1996;26:556–560. - PubMed
-
- Calvert NW, Troy GP, Johnson AG. Laparoscopic cholecystectomy: a good buy? A cost comparison with small-incision (mini) cholecystectomy. Eur J Surg. 2000;166:782–786. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

