Building epidemiological models from R0: an implicit treatment of transmission in networks

Abstract

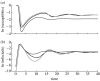
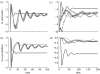
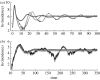
Simple deterministic models are still at the core of theoretical epidemiology despite the increasing evidence for the importance of contact networks underlying transmission at the individual level. These mean-field or 'compartmental' models based on homogeneous mixing have made, and continue to make, important contributions to the epidemiology and the ecology of infectious diseases but fail to reproduce many of the features observed for disease spread in contact networks. In this work, we show that it is possible to incorporate the important effects of network structure on disease spread with a mean-field model derived from individual level considerations. We propose that the fundamental number known as the basic reproductive number of the disease, R0, which is typically derived as a threshold quantity, be used instead as a central parameter to construct the model from. We show that reliable estimates of individual level parameters can replace a detailed knowledge of network structure, which in general may be difficult to obtain. We illustrate the proposed model with small world networks and the classical example of susceptible-infected-recovered (SIR) epidemics.

Figure 1

Comparison of the population dynamics of (a) susceptible and (b) infected proportions for the stochastic model of transmission in a Poisson random network and two mean-field models. The blue lines correspond to a stochastic simulation (with a total number of individuals N=90 000, a probability of transmission per contact per unit of time τ=1, and a mortality rate μ=0.05). The solution of the standard mean-field model 3.1 is in red and that of the modified mean-field model 3.2–3.5 is in green (natural logarithms were used).

Figure 2

Comparison of the population dynamics of (a, c) infected and (b, d) susceptible proportions for two mean-field models and the stochastic model of transmission in a small-world network. Two different values of the transmission parameter were used: (a, b) τ=1 and (c, d) τ=0.25. A set of stochastic simulations are shown in blue (with network parameters ϕ=0.1 and N=90 000). Solutions for the standard mean-field model 3.1 are shown in red and those for the modified mean-field model 3.2–3.5 are shown in green (μ=0.05, r=1, γ=r+μ).

Figure 3

Comparison of the time course of incidence for the stochastic disease model in a small-world network and two mean-field models parameterized from the initial phase of the first epidemic. Two different values of the transmission parameter are shown ((a) τ=1 and (b) τ=0.25). The blue lines correspond to the stochastic network simulations (ϕ=0.1, N=90 000, μ=0.05). We estimated λ from the initial phase of exponential growth of the realizations. From these values, we obtained the effective number of neighbours, $n_{\text{e}}\tau =\hat{\lambda }+1$, and the reproductive number $R_0=\hat{\lambda }/(\tau +\gamma )+1$, which in turn were used to parameterize the standard mean-field model 3.1 corrected with an effective number of neighbours (in red), and the modified mean-field model 3.2–3.5 (in green; see also section 2 in the electronic supplementary material). Natural logarithms were used.

Figure 4

Snapshots of the spatial grid for the stochastic model with the small-world network, for two different values of τ ((a) τ=0.25 and (b) τ=1). The red, blue and black sites correspond to infected, recovered and susceptible individuals, respectively. For initial conditions including a few foci of infection in a completely susceptible population, clusters develop quickly, after a short initial spread that appears exponential. For (a) the lower transmission rates, the clusters interfere most with the further propagation of the disease as most infected individuals are in close contact with recovered and other infected individuals. This difference is apparent by comparing the clusters of infection for the two transmission parameters.