The evolution of condition-dependent sex in the face of high costs
- PMID: 17483405
- PMCID: PMC1931531
- DOI: 10.1534/genetics.107.074203
The evolution of condition-dependent sex in the face of high costs
Abstract
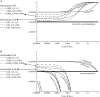
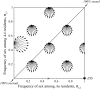
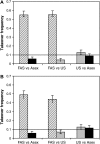
Facultatively sexual organisms often engage in sex more often when in poor condition. We show that such condition-dependent sex carries evolutionary advantages and can explain the evolution of sexual reproduction even when sex entails high costs. Specifically, we show that alleles promoting individuals of low fitness to have sex more often than individuals of high fitness spread through a population. Such alleles are more likely to segregate out of bad genetic backgrounds and onto good genetic backgrounds, where they tend to remain. This "abandon-ship" mechanism provides a plausible model for the evolution and maintenance of facultative sex.
Figures



Similar articles
-
Condition-dependent sex and the rate of adaptation.Am Nat. 2009 Jul;174 Suppl 1:S71-8. doi: 10.1086/599086. Am Nat. 2009. PMID: 19459778
-
Is sex advantageous in adverse environments? A test of the abandon-ship hypothesis.Am Nat. 2013 Dec;182(6):718-25. doi: 10.1086/673476. Epub 2013 Oct 9. Am Nat. 2013. PMID: 24231534
-
The evolutionary enigma of sex.Am Nat. 2009 Jul;174 Suppl 1:S1-S14. doi: 10.1086/599084. Am Nat. 2009. PMID: 19441962 Review.
-
Abandoning the ship using sex, dispersal or dormancy: multiple escape routes from challenging conditions.Philos Trans R Soc Lond B Biol Sci. 2018 Oct 5;373(1757):20170424. doi: 10.1098/rstb.2017.0424. Philos Trans R Soc Lond B Biol Sci. 2018. PMID: 30150222 Free PMC article.
-
Sexual conflict and speciation.Philos Trans R Soc Lond B Biol Sci. 1998 Feb 28;353(1366):261-74. doi: 10.1098/rstb.1998.0208. Philos Trans R Soc Lond B Biol Sci. 1998. PMID: 9533125 Free PMC article. Review.
Cited by
-
Different photoperiodic responses in diapause induction can promote the maintenance of genetic diversity via the storage effect in Daphnia pulex.Proc Biol Sci. 2024 Feb 14;291(2016):20231860. doi: 10.1098/rspb.2023.1860. Epub 2024 Feb 14. Proc Biol Sci. 2024. PMID: 38351804 Free PMC article.
-
What drives the evolution of condition-dependent recombination in diploids? Some insights from simulation modelling.Philos Trans R Soc Lond B Biol Sci. 2017 Dec 19;372(1736):20160460. doi: 10.1098/rstb.2016.0460. Philos Trans R Soc Lond B Biol Sci. 2017. PMID: 29109223 Free PMC article.
-
Errors in mutagenesis and the benefit of cell-to-cell signalling in the evolution of stress-induced mutagenesis.R Soc Open Sci. 2017 Nov 1;4(11):170529. doi: 10.1098/rsos.170529. eCollection 2017 Nov. R Soc Open Sci. 2017. PMID: 29291054 Free PMC article.
-
Higher rates of sex evolve in spatially heterogeneous environments.Nature. 2010 Nov 4;468(7320):89-92. doi: 10.1038/nature09449. Epub 2010 Oct 13. Nature. 2010. PMID: 20944628
-
Seasonal variation of genotypes and reproductive plasticity in a facultative clonal freshwater invertebrate animal (Hydra oligactis) living in a temperate lake.Ecol Evol. 2022 Jul 14;12(7):e9096. doi: 10.1002/ece3.9096. eCollection 2022 Jul. Ecol Evol. 2022. PMID: 35845371 Free PMC article.
References
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Research Materials

