Mechanical properties of inner-arm dynein-f (dynein I1) studied with in vitro motility assays

Abstract

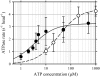
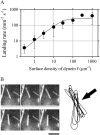
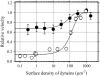
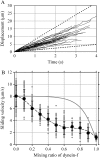
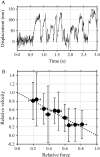
Inner-arm dynein-f of Chlamydomonas flagella is a heterodimeric dynein. We performed conventional in vitro motility assays showing that dynein-f translocates microtubules at the comparatively low velocity of approximately 1.2 microm/s. From the dependence of velocity upon the surface density of dynein-f, we estimate its duty ratio to be 0.6-0.7. The relation between microtubule landing rate and surface density of dynein-f are well fitted by the first-power dependence, as expected for a processive motor. At low dynein densities, progressing microtubules rotate erratically about a fixed point on the surface, at which a single dynein-f molecule is presumably located. We conclude that dynein-f has high processivity. In an axoneme, however, slow and processive dynein-f could impede microtubule sliding driven by other fast dyneins (e.g., dynein-c). To obtain insight into the in vivo roles of dynein-f, we measured the sliding velocity of microtubules driven by a mixture of dyneins -c and -f at various mixing ratios. The velocity is modulated as a function of the ratio of dynein-f in the mixture. This modulation suggests that dynein-f acts as a load in the axoneme, but force pushing dynein-f molecules forward seems to accelerate their dissociation from microtubules.

FIGURE 1

Purification and molecular morphology of dynein-f. (A) sodium dodecyl sulfate-polyacrylamide gel electrophoresis (left lane: 3% polyacrylamide, right lane: 5%–20%) of purified dynein-f, whose heavy chains (I1α and I1β) run at 450 kDa. Three intermediate chains (IC140, IC138, and IC97) are clearly visible in the gel. A few light chains (LCs) are also visible. (B) Field of negatively stained dynein-f molecules in the absence of nucleotide showing tails attached to two globular heads. Scale bar, 50 nm. Gallery of typical molecules showing the two-headed configuration. Scale bar, 20 nm.

FIGURE 2

Structure of dynein-f. (A) Class averages showing a variety of head-head configurations (upper two globular domains) and the asymmetric tail domain (pointing downwards). (B) Class averages showing substructural detail within the tail domain. A small distal domain is indicated (arrow). (C) Class average showing the head domain after a second round of alignment using just the part of each image containing the head. This class is strikingly similar to right views of dynein-c in the absence of nucleotide (17), and the corresponding positions of dynein-c's stalk (arrowhead) and tail (arrow) domains are indicated. The number of images in each class is shown in the lower right corner. The number of individual molecules aligned and classified is n = 578 (A and B) and n = 1566 (C). Scale bar, A and B: 20 nm, C: 10 nm.

FIGURE 3

ATPase rate of dynein-f. Basal ATPase activities of dynein-f (solid circles) and -c (open circles) at various ATP concentrations. Error bars indicate standard deviations. The curves are fits by the Michaelis-Menten equation: maximum ATPase rate, v_max = 3.3 ± 0.2 s⁻¹ head⁻¹ and K_m = 3.3 ± 0.7 μM for dynein-f (solid curve): v_max = 4.4 ± 0.04 s⁻¹ head⁻¹, and K_m = 31.4 ± 1.1 μM for dynein-c (dashed curve).

FIGURE 4

Dependence of microtubule landing rate on the density of dynein-f-coated glass surfaces. (A) The solid curve is the fit to the Poisson model for a single molecule of dynein-f sufficing to move a microtubule: k(ρ) = C₀ (1 − e^−Aρ), where k(ρ) is landing rate at dynein-f density ρ and A is the product of microtubule length and twice the reach of dynein-f; these values are C₀ = 260 mm⁻² s⁻¹, A = 0.04 μm². (B) Video sequence and tracings of images showing thermally driven rotation of a microtubule around a nodal point while also moving progressively (dynein-f density: 1 molecule per μm²). Tracings were obtained from successive video images at 1/3-s intervals. The arrow indicates the fixed point on the surface, about which the microtubule rotated. Scale bar, 5 μm.

FIGURE 5

ATP concentration dependence of sliding velocity of microtubules on dynein-f-coated surfaces. Error bars indicate standard deviations for velocities. The curve is a fit by the Michaelis-Menten equation: the curve has maximal gliding velocity, V_max = 1.6 ± 0.1 μm/s, and K_m = 55 ± 11 μM. Gray dots indicate original data.

FIGURE 6

Relationship between velocity of microtubule sliding and surface density of dynein. Error bars indicate standard deviations for dynein-f (solid circles) and dynein-c (open circles). Solid curves are fits to V_max (1 − e^−Aρf)/(1 − e^−Aρ) in which V_max, ρ, f, and A are, respectively, the maximal velocity, the density of dyneins, the duty ratio, and the product of microtubule length and twice the reach of a dynein molecule; values: for dynein-f V_max = 0.99 ± 0.37 μm/s, V_min = 0.62 ± 0.32 μm/s, f = V_min/V_max = 0.63, A = 0.027 ± 0.01 μm² and for dynein-c V_max = 5.1 μm/s, V_min = 0.7 μm/s, f = V_min/V_max = 0.14, A = 0.053 μm². The data for dynein-c are replotted from Sakakibara et al. (15).

FIGURE 7

Microtubule sliding driven by mixtures of dyneins -f and -c. (A) Trajectories of individual microtubules driven by dynein-f and -c at a mixing ratio of 0.5 were plotted as a function of time. Dotted lines indicate the displacements with constant velocity of 8 (upper, corresponding to the maximal velocity driven by dynein-c alone) and 1.2 (lower, corresponding to the maximal velocity driven by dynein-f alone) μm/s, which correspond to the maximal velocity driven by dynein-c and dynein-f, respectively. (B) Sliding velocities for mixtures of dynein-f and -c. Error bars indicate standard deviations. The gray solid line is the estimated velocity driven by dynein-c alone. Gray solid circles are raw data points at various mixing ratios. The distributions indicate unimodal distributions of velocity at each mixing ratio. The dashed curve is the quartic equation to describe the relation. The coefficient of determination, the measure of how well a regression model describes the data, was 0.998.

FIGURE 8

The force-velocity relationship of microtubule sliding driven by ensembles of dynein-c. (A) A typical record of force and movement of a microtubule driven by ensembles of dynein-c in the presence of 200 μM ATP. (B) The force-velocity curve was almost linear: i.e., the velocity decreased linearly with increasing load. Since the microtubules often dissociate before slowing down substantially, the force-velocity curves do not reach the force axis (zero velocity). A linear fit to the data gives an extrapolated maximal velocity of 1.5 μm/s, agreeing with those for microtubule's gliding measured in in vitro motility assays.

FIGURE 9

Relative drag coefficient of dynein-f calculated as a function of velocity. As shown in Fig. 7, the reduction of the velocity of microtubules driven by dynein-c is due to the presence of dynein-f. Based upon the linear force-velocity relation of dynein-c in Fig. 8 and the previous study (25), the reduction of the velocity is converted into the load on dynein-c. We calculated the relative drag coefficient of dynein-f by dividing the load by the velocity measured and the mixing ratio of dynein-f and then plotted this coefficient with respect to microtubule sliding velocity. Error bars indicate standard deviations. The gray curve is obtained using the fit of a quartic equation to the relationship between the velocity and the density of dynein-f (Fig. 7, dashed curve).