Modelling calcium microdomains using homogenisation
- PMID: 17499276
- PMCID: PMC1991275
- DOI: 10.1016/j.jtbi.2007.03.019
Modelling calcium microdomains using homogenisation
Abstract
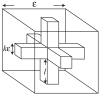
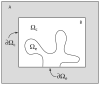
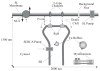
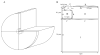
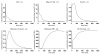
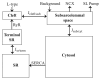
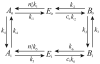
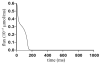
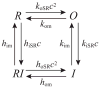
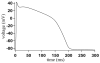
Microdomains of calcium (i.e., areas on the nanometer scale that have qualitatively different calcium concentrations from that in the bulk cytosol) are known to be important in many situations. In cardiac cells, for instance, a calcium microdomain between the L-type channels and the ryanodine receptors, the so-called diadic cleft, is where the majority of the control of calcium release occurs. In other cell types that exhibit calcium oscillations and waves, the importance of microdomains in the vicinity of clusters of inositol trisphosphate receptors, or between the endoplasmic reticulum (ER) and other internal organelles or the plasma membrane, is clear. Given the limits of computational power, it is not currently realistic to model an entire cellular cytoplasm by incorporating detailed structural information about the ER throughout the entire cytoplasm. Hence, most models use a homogenised approach, assuming that both cytoplasm and ER coexist at each point of the domain. Conversely, microdomain models can be constructed, in which detailed structural information can be incorporated, but, until now, methods have not been developed for linking such a microdomain model to a model at the level of the entire cell. Using the homogenisation approach we developed in an earlier paper [Goel, P., Friedman, A., Sneyd, J., 2006. Homogenization of the cell cytoplasm: the calcium bidomain equations. SIAM J. Multiscale Modeling Simulation, in press] we show how a multiscale model of a calcium microdomain can be constructed. In this model a detailed model of the microdomain (in which the ER and the cytoplasm are separate compartments) is coupled to a homogenised model of the entire cell in a rigorous way. Our method is illustrated by a simple model of the diadic cleft of a cardiac half-sarcomere.
Figures
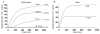







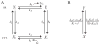
Similar articles
-
A novel mechanism of tandem activation of ryanodine receptors by cytosolic and SR luminal Ca2+ during excitation-contraction coupling in atrial myocytes.J Physiol. 2017 Jun 15;595(12):3835-3845. doi: 10.1113/JP273611. Epub 2017 Feb 1. J Physiol. 2017. PMID: 28028837 Free PMC article.
-
Pacemaking, arrhythmias, inotropy and hypertrophy: the many possible facets of IP3 signalling in cardiac myocytes.J Physiol. 2007 Jun 15;581(Pt 3):883-4. doi: 10.1113/jphysiol.2007.133819. Epub 2007 Apr 19. J Physiol. 2007. PMID: 17446217 Free PMC article. No abstract available.
-
Modeling calcium waves in cardiac myocytes: importance of calcium diffusion.Front Biosci (Landmark Ed). 2010 Jan 1;15(2):661-80. doi: 10.2741/3639. Front Biosci (Landmark Ed). 2010. PMID: 20036839 Free PMC article.
-
Sarco-Endoplasmic Reticulum Calcium Release Model Based on Changes in the Luminal Calcium Content.Adv Exp Med Biol. 2020;1131:337-370. doi: 10.1007/978-3-030-12457-1_14. Adv Exp Med Biol. 2020. PMID: 31646517 Review.
-
Alterations of the Endoplasmic Reticulum (ER) Calcium Signaling Molecular Components in Alzheimer's Disease.Cells. 2020 Dec 1;9(12):2577. doi: 10.3390/cells9122577. Cells. 2020. PMID: 33271984 Free PMC article. Review.
Cited by
-
A multiscale MD-FE model of diffusion in composite media with internal surface interaction based on numerical homogenization procedure.Comput Methods Appl Mech Eng. 2014 Feb 1;269:123-138. doi: 10.1016/j.cma.2013.11.010. Comput Methods Appl Mech Eng. 2014. PMID: 24578582 Free PMC article.
-
A computational model of spatio-temporal cardiac intracellular calcium handling with realistic structure and spatial flux distribution from sarcoplasmic reticulum and t-tubule reconstructions.PLoS Comput Biol. 2017 Aug 31;13(8):e1005714. doi: 10.1371/journal.pcbi.1005714. eCollection 2017 Aug. PLoS Comput Biol. 2017. PMID: 28859079 Free PMC article.
-
Modelling compartmentalization towards elucidation and engineering of spatial organization in biochemical pathways.Sci Rep. 2017 Sep 21;7(1):12057. doi: 10.1038/s41598-017-11081-8. Sci Rep. 2017. PMID: 28935941 Free PMC article.
-
Data-based theoretical identification of subcellular calcium compartments and estimation of calcium dynamics in cardiac myocytes.J Physiol. 2012 Sep 15;590(18):4423-46. doi: 10.1113/jphysiol.2012.228791. Epub 2012 Apr 30. J Physiol. 2012. PMID: 22547631 Free PMC article.
-
Optimal microdomain crosstalk between endoplasmic reticulum and mitochondria for Ca2+ oscillations.Sci Rep. 2015 Jan 23;5:7984. doi: 10.1038/srep07984. Sci Rep. 2015. PMID: 25614067 Free PMC article.
References
-
- Apell HJ. Electrogenic properties of the Na,K pump. J Membr Biol. 1989;110:103–114. - PubMed
-
- Augustine GJ, Santamaria F, Tanaka K. Local Calcium Signaling in Neurons. Neuron. 2003;40:331–346. - PubMed
-
- Bensoussan A, Lions JL, Papanicolaou G. Asymptotic Analysis for Periodic Structures. North Holland Science Publishers; New York: 1978.
-
- Bers DM. Excitation-Contraction Coupling and Cardiac Contractile Force. 2. Kluwer Academic Publishers; 2001.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

