Microscopic diffusion and hydrodynamic interactions of hemoglobin in red blood cells

Abstract

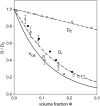
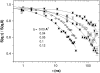
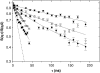
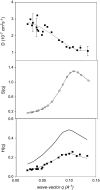
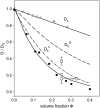
The cytoplasm of red blood cells is congested with the oxygen storage protein hemoglobin occupying a quarter of the cell volume. The high protein concentration leads to a reduced mobility; the self-diffusion coefficient of hemoglobin in blood cells is six times lower than in dilute solution. This effect is generally assigned to excluded volume effects in crowded media. However, the collective or gradient diffusion coefficient of hemoglobin is only weakly dependent on concentration, suggesting the compensation of osmotic and friction forces. This would exclude hydrodynamic interactions, which are of dynamic origin and do not contribute to the osmotic pressure. Hydrodynamic coupling between protein molecules is dominant at short time- and length scales before direct interactions are fully established. Employing neutron spin-echo-spectroscopy, we study hemoglobin diffusion on a nanosecond timescale and protein displacements on the scale of a few nanometers. A time- and wave-vector dependent diffusion coefficient is found, suggesting the crossover of self- and collective diffusion. Moreover, a wave-vector dependent friction function is derived, which is a characteristic feature of hydrodynamic interactions. The wave-vector and concentration dependence of the long-time self-diffusion coefficient of hemoglobin agree qualitatively with theoretical results on hydrodynamics in hard spheres suspensions. Quantitative agreement requires us to adjust the volume fraction by including part of the hydration shell: Proteins exhibit a larger surface/volume ratio compared to standard colloids of much larger size. It is concluded that hydrodynamic and not direct interactions dominate long-range molecular transport at high concentration.

FIGURE 1

Normalized long-time diffusion coefficients D(Φ)/D₀: (triangles) collective diffusion coefficient D_c of hemoglobin in solution (light scattering), (dash-dotted line) fit to D_c/D₀ = 1+ B₁ · Φ with B₁ = −0.76. Tracer diffusions coefficients, D_t, of hemoglobin in solution (small open squares) (29,37) and in red blood cells (NMR): large open square (8), and of myoglobin in solution (solid circles) (11,37), (dash-dotted line) fit of D_t to an exponential function with Φ₀ = 0.15, (solid line) exponential fit to the osmotic compressibility, κ_os, of hemoglobin and myoglobin yielding Φ₀ = 0.12 (29,30).

FIGURE 2

Normalized intermediate scattering functions S(q,τ)/S(q,0) of hemoglobin in RBCs on a log-timescale, measured with the neutron spin-echo-spectrometer IN 15 (Institut Laue-Langevin in Grenoble) at several wave-vectors q; (lines) fits of the data to a single exponential function as described in the text.

FIGURE 3

Semilogarithmic plot ln[S(q,τ)/S(q,0)] of the intermediate scattering function shown in Fig. 2 at the same wave-vectors q = 0.03, 0.04, 0.05, 0.1, and 0.12 Å⁻¹. The lines are fits of the data to a single exponential function. The dashed line at q = 0.12 Å⁻¹ refers to the fast component reflecting short-time diffusion.

FIGURE 4

(Top) Generalized diffusion coefficient D(q,τ) (Eq. 4) of hemoglobin in RBCs at 37°C in D₂O-buffer C; the line is drawn to guide the eye. (Middle) Interparticle structure factor S(q) of hemoglobin in RBCs, MSA calculations adjusted from Krueger et al. (5,32). (Bottom) Theoretical short-time hydrodynamic function of a hard-sphere colloid H(q) at Φ = 0.25 adjusted from Beenakker and Mazur (16), experimental H(q) = D(q)/D₀ · S(q); the solid line through data is the prediction H(q)/2.1 adjusted to fit the experimental data.

FIGURE 5

Normalized relative diffusion coefficients D(Φ)/D₀: (open triangles) D_c, collective diffusion coefficient of hemoglobin in solution (dynamic light scattering) from Fig. 1, neutron scattering results at q = 0.12 Å⁻¹: (open circles) suggested long-time diffusion coefficient of hemoglobin in blood cells and of hemoglobin in solution (open diamonds) at Φ = 0.25. (Open squares) Short-time diffusion coefficient of hemoglobin in RBCs from Fig. 3. (Solid circles) of myoglobin in solution (31) and (dash-dotted line) exponential fit to D_t (Fig. 1) yielding Φ₀ = 0.15, (dashed line) theoretical short-time self-diffusion coefficient, for hard sphere suspensions (16,17,35), and (solid line) theoretical long-time self-diffusion coefficient, for hard sphere suspensions (17).