Chlorophyll ring deformation modulates Qy electronic energy in chlorophyll-protein complexes and generates spectral forms

Abstract

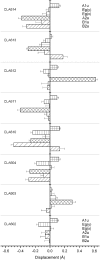
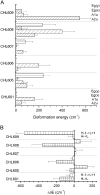
The possibility that the chlorophyll (chl) ring distortions observed in the crystal structures of chl-protein complexes are involved in the transition energy modulation, giving rise to the spectral forms, is investigated. The out-of-plane chl-macrocycle distortions are described using an orthonormal set of deformations, defined by the displacements along the six lowest-frequency, out-of-plane normal coordinates. The total chl-ring deformation is the linear combination of these six deformations. The two higher occupied and the two lower unoccupied chl molecular orbitals, which define the Q(y) electronic transition, have the same symmetry as four of the six out-of-plane lowest frequency modes. We assume that a deformation along the normal-coordinate having the same symmetry as a given molecular orbital will perturb that orbital and modify its energy. The changes in the chl Q(y) transition energies are evaluated in the Peridinin-Chl-Protein complex and in light harvesting complex II (LHCII), using crystallographic data. The macrocycle deformations induce a distribution of the chl Q(y) electronic energy transitions which, for LHCII, is broader for chla than for chlb. This provides the physical mechanism to explain the long-held view that the chla spectral forms in LHCII are both more numerous and cover a wider energy range than those of chlb.

FIGURE 1

The observed chla atoms out-of-plane displacements. The distances of all the atoms comprising the chl macrocycle with respect to the nitrogen plane NA-NB-NC are shown in an (x,z) projection. For clarity, the mirror image with respect to the CHC atom of the II, III, and V rings is shown. The Mg atom is also displayed (pentagon). The coordinates of the chl atoms are those given by Chow et al. (7). The nomenclature is according to PDB.

FIGURE 2

Out-of-plane displacements for isolated chla and chlb. The values are obtained by NSD analysis of the crystallographic data (7) using the minimal set of normal modes ((38), Materials and Methods). These modes have the symmetry types shown in figure (D_4h group nomenclature).

FIGURE 3

Energy contributions due to chl macrocycle deformations. (A) Deformation energies for the normal modes of the minimal set used to decompose the macrocycle deformation and having the same symmetry of the HOMO (a_1u), HOMO-1 (a_2u), LUMO (e_g(x)), and LUMO+1 (e_g(y)). (B) Deformation-induced perturbation of the HOMO → LUMO and HOMO-1 → LUMO+1 energy gaps for isolated chla and chlb obtained using the deformation energies of panel A.

FIGURE 4

Out-of-plane displacements for PCP chlorophylls. The values are obtained by NSD analysis of the crystallographic data (32) using the minimal set of normal modes ((38), Materials and Methods). These modes have the symmetry types shown in figure (D_4h group nomenclature). For each chl molecule, the values are the mean of the results obtained analyzing the chl crystal coordinates of three different PCP monomers. The error bars are also shown.

FIGURE 5

Energy contributions due to PCP chla macrocycle deformations. (A) Deformation energies for the normal modes of the minimal set used to decompose the macrocycle deformation and having the same symmetry of the HOMO (a_1u), HOMO-1 (a_2u), LUMO (e_g(x)), and LUMO+1 (e_g(y)). (B) Deformation induced perturbation of the HOMO → LUMO and HOMO-1 → LUMO+1 energy gaps for PCP chla obtained using the deformation energies. All the values are obtained using the mean values of Fig. 4.

FIGURE 6

The PCP chla Q_y transitions in the presence of nonspecific solvatochromic effect. The wavelength red shift due to solvatochromic effect is calculated using Eq. 8 (5), with the dielectric constant D = 5, as a function of the refractive index n. The horizontal line is the wavelength of the RT absorption maximum of the chla in PCP complex (667.5 nm, (54)). The two PCP chla without excitonic contribution, ——; the two PCP chla with the excitonic contribution, ⋯⋯⋯. Using D = 20, very small changes are observed (not shown).

FIGURE 7

Linear plot of the LHCII chla macrocycle. The atoms comprising the chla macrocycle are shown in an (x,z) projection with nitrogen NA, NB, and NC (PDB nomenclature) that lie on the (x,y) plane. The Mg atom is also displayed (pentagon). The chl molecules are shown in a linearized mode, after taking the mirror image of the II, III, and V rings with respect to the CHC atom (PDB nomenclature).

FIGURE 8

Linear plot of the LHCII chlb macrocycle. The atoms comprising the chlb macrocycle are shown in an (x,z) projection with nitrogen NA, NB, and NC (PDB nomenclature) that lie on the (x,y) plane. The Mg atom is also displayed (pentagon). The chl molecules are shown in a linearized mode, after taking the mirror image of the II, III, and V rings with respect to the CHC atom (PDB nomenclature).

FIGURE 9

Out-of-plane displacements for the LHCII chlorophylls a. The values are obtained by NSD analysis of the crystallographic data (35) using the minimal set of normal modes ((38), Materials and Methods). These modes have the symmetry types shown in figure (D_4h group nomenclature). For each chl molecule, the values are the mean of the results obtained analyzing the chla crystal coordinates of three different LHCII trimers. The evaluated errors are also shown. On the basis of the displacements and using Eq. 1, the total deformation energy E_D (cm⁻¹) for each chl can be evaluated: and

FIGURE 10

Out-of-plane displacements for the LHCII chlorophylls b. The values are obtained by NSD analysis of the crystallographic data (35) using the minimal set of normal modes ((38) Materials and Methods). These modes have the symmetry types shown in figure (D_4h group nomenclature). For each chl molecule, the values are the mean of the results obtained analyzing the chlb crystal coordinates of three different LHCII trimers. The evaluated errors are also shown. On the basis of the displacements and using Eq. 1, the total deformation energy E_D (cm⁻¹) for each chl can be evaluated: and

FIGURE 11

Energy contributions due to LHCII chla macrocycle deformations. (A) Deformation energies for the normal modes of the minimal set used to decompose the macrocycle deformation and having the same symmetry of the HOMO (a_1u), HOMO-1 (a_2u), LUMO (e_g(x)), and LUMO+1 (e_g(y)). (B) Deformation-induced perturbation of the HOMO → LUMO and HOMO-1 → LUMO+1 energy gaps for LHCII chla obtained using the deformation energies. All the values are obtained using the mean values of the out-of-plane displacements of Fig. 9. The displacement errors are used to determine the uncertainties on deformation energies (A) as well as energy gaps perturbation (B). These uncertainties are shown as error bars.

FIGURE 12

Energy contributions due to LHCII chlb macrocycle deformations. (A) Deformation energies for the normal modes of the minimal set used to decompose the macrocycle deformation and having the same symmetry of the HOMO (a_1u), HOMO-1 (a_2u), LUMO (e_g(x)), and LUMO+1 (e_g(y)). (B) Deformation induced perturbation of the HOMO → LUMO and HOMO-1 → LUMO+1 energy gaps for LHCII chlb obtained using the deformation energies. All the values are obtained using the mean values of the out-of-plane displacements of Fig. 10. The displacement errors are used to determine the uncertainties on deformation energies (A) as well as energy-gap perturbation (B). These uncertainties are shown as error bars.

FIGURE 13

The intrinsic-structural Q_y transitions of the LHCII chls. The wavelengths are obtained as eigenvalues of the Gouterman matrix (Eq. 5) as outlined in Materials and Methods, using the data of Fig. 11 B and Fig. 12 B and the two reference sets for both chla and chlb obtained when the unperturbed energy gaps are considered as representatives of chl in solution ({18,735; 29,472; 6742} for chla and {18,735; 29,472; 6215} for chlb). The shaded areas represent the unperturbed wavelengths of chla and b whereas the open areas are the changes related to macrocycle deformation. The uncertainties are obtained propagating the uncertainties of the energy gap perturbations induced by the macrocycle deformations.

FIGURE 14

The LHCII chla Q_y transitions in the presence of nonspecific solvatochromic effect. The wavelength red shift due to solvatochromic effect is calculated using Eq. 8 (5), with the dielectric constant D = 5, as a function of the refractive index n. Using D = 20, very small changes are observed (not shown).