A kinetic model of single and clustered IP3 receptors in the absence of Ca2+ feedback
- PMID: 17526578
- PMCID: PMC1929031
- DOI: 10.1529/biophysj.107.108795
A kinetic model of single and clustered IP3 receptors in the absence of Ca2+ feedback
Abstract
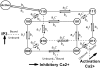
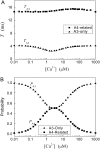
Ca2+ liberation through inositol 1,4,5-trisphosphate receptor (IP3R) channels generates complex patterns of spatiotemporal cellular Ca2+ signals owing to the biphasic modulation of channel gating by Ca2+ itself. These processes have been extensively studied in Xenopus oocytes, where imaging studies have revealed local Ca2+ signals ("puffs") arising from clusters of IP3R, and patch-clamp studies on isolated oocyte nuclei have yielded extensive data on IP3R gating kinetics. To bridge these two levels of experimental data, we developed an IP3R model and applied stochastic simulation and transition matrix theory to predict the behavior of individual and clustered IP3R channels. The channel model consists of four identical, independent subunits, each of which has an IP3-binding site together with one activating and one inactivating Ca2+-binding site. The channel opens when at least three subunits undergo a conformational change to an "active" state after binding IP3 and Ca2+. The model successfully reproduces patch-clamp data; including the dependence of open probability, mean open duration, and mean closed duration on [IP3] and [Ca2+]. Notably, the biexponential distribution of open-time duration and the dependence of mean open time on [Ca2+] are explained by populations of openings involving either three or four active subunits. As a first step toward applying the single IP3R model to describe cellular responses, we then simulated measurements of puff latency after step increases of [IP3]. Assuming that stochastic opening of a single IP3R at basal cytosolic [Ca2+] and any given [IP3] has a high probability of rapidly triggering neighboring channels by calcium-induced calcium release to evoke a puff, optimal correspondence with experimental data of puff latencies after photorelease of IP3 was obtained when the cluster contained a total of 40-70 IP3Rs.
Figures






Similar articles
-
Inositol 1,4,5-trisphosphate [correction of tris-phosphate] activation of inositol trisphosphate [correction of tris-phosphate] receptor Ca2+ channel by ligand tuning of Ca2+ inhibition.Proc Natl Acad Sci U S A. 1998 Dec 22;95(26):15821-5. doi: 10.1073/pnas.95.26.15821. Proc Natl Acad Sci U S A. 1998. PMID: 9861054 Free PMC article.
-
Dynamic clustering of IP3 receptors by IP3.Biochem Soc Trans. 2012 Apr;40(2):325-30. doi: 10.1042/BST20110772. Biochem Soc Trans. 2012. PMID: 22435806 Review.
-
An allosteric model of the inositol trisphosphate receptor with nonequilibrium binding.Phys Biol. 2014 Aug 14;11(5):056001. doi: 10.1088/1478-3975/11/5/056001. Phys Biol. 2014. PMID: 25118617
-
A computational analysis of localized Ca2+-dynamics generated by heterogeneous release sites.Bull Math Biol. 2009 Oct;71(7):1543-79. doi: 10.1007/s11538-009-9413-y. Epub 2009 May 14. Bull Math Biol. 2009. PMID: 19440797
-
Analysis of IP3 receptors in and out of cells.Biochim Biophys Acta. 2012 Aug;1820(8):1214-27. doi: 10.1016/j.bbagen.2011.10.004. Epub 2011 Oct 14. Biochim Biophys Acta. 2012. PMID: 22033379 Review.
Cited by
-
'Eventless' InsP3-dependent SR-Ca2+ release affecting atrial Ca2+ sparks.J Physiol. 2013 Apr 15;591(8):2103-11. doi: 10.1113/jphysiol.2012.247288. Epub 2013 Feb 4. J Physiol. 2013. PMID: 23381902 Free PMC article.
-
Intra-cluster percolation of calcium signals.PLoS One. 2010 Feb 18;5(2):e8997. doi: 10.1371/journal.pone.0008997. PLoS One. 2010. PMID: 20174630 Free PMC article.
-
Data-driven modeling of mitochondrial dysfunction in Alzheimer's disease.Cell Calcium. 2018 Dec;76:23-35. doi: 10.1016/j.ceca.2018.09.003. Epub 2018 Sep 12. Cell Calcium. 2018. PMID: 30248575 Free PMC article.
-
Picomolar sensitivity to inositol trisphosphate in Xenopus oocytes.Cell Calcium. 2015 Nov;58(5):511-7. doi: 10.1016/j.ceca.2015.08.003. Epub 2015 Aug 20. Cell Calcium. 2015. PMID: 26344104 Free PMC article.
-
IP3 receptor signaling and endothelial barrier function.Cell Mol Life Sci. 2017 Nov;74(22):4189-4207. doi: 10.1007/s00018-017-2624-8. Epub 2017 Aug 12. Cell Mol Life Sci. 2017. PMID: 28803370 Free PMC article. Review.
References
-
- Taylor, C. W., P. C. da Fonseca, and E. P. Morris. 2004. IP3 receptors: the search for structure. Trends Biochem. Sci. 29:210–219. - PubMed
-
- Bosanac, I., J. R. Alattia, T. K. Mal, J. Chan, S. Talarico, F. K. Tong, K. I. Tong, F. Yoshikawa, T. Furuichi, M. Iwai, T. Michikawa, K. Mikoshiba, and M. Ikura. 2002. Structure of the inositol 1,4,5-trisphosphate receptor binding core in complex with its ligand. Nature. 420:696–700. - PubMed
-
- Bezprozvanny, I. 2005. The inositol 1,4,5-trisphosphate receptors. Cell Calcium. 38:261–272. - PubMed
-
- Bezprozvanny, I., J. Watras, and B. E. Ehrlich. 1991. Bell-shaped calcium-response curves of Ins(1,4,5)P3- and calcium-gated channels from endoplasmic reticulum of cerebellum. Nature. 351:751–754. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials
Miscellaneous

