Effects of diffusion weighting schemes on the reproducibility of DTI-derived fractional anisotropy, mean diffusivity, and principal eigenvector measurements at 1.5T

Abstract

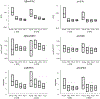
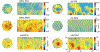
Diffusion tensor imaging (DTI) is used to study tissue composition and architecture in vivo. To increase the signal to noise ratio (SNR) of DTI contrasts, studies typically use more than the minimum of 6 diffusion weighting (DW) directions or acquire repeated observations of the same set of DW directions. Simulation-based studies have sought to optimize DTI acquisitions and suggest that increasing the directional resolution of a DTI dataset (i.e., the number of distinct directions) is preferable to repeating observations, in an equal scan time comparison. However, it is not always clear how to translate these recommendations into practice when considering physiological noise and scanner stability. Furthermore, the effect of different DW schemes on in vivo DTI findings is not fully understood. This study characterizes how the makeup of a DW scheme, in terms of the number of directions, impacts the precision and accuracy of in vivo fractional anisotropy (FA), mean diffusivity (MD), and principal eigenvector (PEV) findings. Orientation dependence of DTI reliability is demonstrated in vivo and a principled theoretical framework is provided to support and interpret findings with simulation results. As long as sampling orientations are well balanced, differences in DTI contrasts due to different DW schemes are shown to be small relative to intra-session variability. These differences are accentuated at low SNR, while minimized at high SNR. This result suggests that typical clinical studies, which use similar protocols but different well-balanced DW schemes, are readily comparable within the experimental precision.

Fig. A1.

Illustration of angular error metrics. Angular variability (AV, panel A) is defined as the mean angle between observed vectors and the mean vector, while angular bias (AB, panel B) is defined as the angle between the mean vector and a gold standard (GS) reference vector. The mean angular difference (MAD, panel C) is defined as the mean angle between observed vectors and a gold standard. Ovals indicate the mean angle of the encompassed arcs.

Fig. 1.

Minimum potential energy (PE) partitions of the Jones30 DW scheme. The optimal PE partitions (left) are evenly distributed as indicated by the shading which is proportional to the area of the spherical Voronoi tessellations of the DW directions. The realized directions are distinct (right) from the specified ones (left) because the gradient tables are corrected for subject motion. The right panel shows 30 clusters, where each cluster represents a specified DW direction and consists of three sub-clusters which represent realized DW directions from each session. The separation of the sub-clusters shows the inter-session effects, while the distribution of the symbols shows the intra-session effects. Large ovals indicate the subset of the Jones30 that was used to construct the PE₆ partition.

Fig. 2.

Representative colormaps of the PEV orientation obtained with each of the PE partitioned DW schemes at 1 STE (left). For comparison, a colormap and a FA map computed with all acquired data from one session (15 STEs) are shown at right.

Fig. 3.

Observed FA within ROIs by DW scheme. For each DW scheme, the mean FA within each ROI (indicated at right, scc=splenium of the corpus callosum, ic=internal capsule, cs=centrum semiovale, gp=globus pallidus, and put=putamen) and each session are shown. Horizontal lines indicate the mean over three sessions of the Jones30 observations for the corresponding STE and ROI.

Fig. 4.

Observed MD within ROIs by DW scheme. For each diffusion weighting scheme, MD within two ROIs (indicated at right, scc=splenium of the corpus callosum and put=putamen) and each session are shown. Horizontal lines indicate the mean over three sessions of the Jones30 observations for the corresponding STE and ROI.

Fig. 5.

Observed MAD within ROIs by DW scheme. For each diffusion weighting scheme, MAD within two ROIs (indicated at right, scc=splenium of the corpus callosum and put=putamen) and each session are shown. Horizontal lines indicate the mean over three sessions of the Jones30 observations for the corresponding STE and ROI.

Fig. 6.

Directional sensitivity is evident for FA variability. The precision of FA (standard deviation) is plotted as a function of the underlying PEV orientation (spherical coordinates) for all the voxels in the brain with FA> 0.25. The precision of FA measurements with the PE₆ scheme (panel A) showed a noticeably greater dependence on orientation than the Jones30 scheme (panel B). The differences (panel C) between the schemes highlight pockets of poor FA precision that correspond well to the sparse sampling of the PE₆ scheme. Black markers indicate the specified DW directions.

Fig. 7.

Experimental directional sensitivity and bias for the PE₆ relative to Jones30 scheme. Differences in the bias magnitude (Δ|bias|) and standard deviations (Δσ) are plotted for FA (first row) and MD (second row). For the PEV, angular bias (AB) and variability (AV) are reported (third row). The 6 directions of the PE₆ scheme are indicated by circled markers. To aid in interpretation, the small spheres to the left of the polar plots display the same data as the corresponding polar plot.

Fig. 8.

PEV orientation dependence for derived contrasts. The minimum and maximum of each rectangle correspond to the 2.5% and 97.5% quantile differences (95% range of differences) of orientation dependence maps (e.g., as shown in Fig. 7) between the indicated DW scheme and Jones30 scheme. Central horizontal lines represent the median difference.

Fig. 9.

Simulated directional sensitivity and bias for the PE₆ relative to Jones30 DW scheme. Differences in the bias magnitude (Δ|bias|) and standard deviations (Δσ) are plotted for FA (first row) and MD (second row). For the PEV, angular bias (AB) and variability (AV) are reported (third row). The 6 directions of the 6 DW direction schemes are indicated by circled markers. To aid in interpretation, the small spheres to the left of the polar plots display the same data as the corresponding polar plot.

Fig. 10.

Simulated impact of DW scheme on tensor metrics for the PE₆ scheme relative to the Jones30 scheme. Differential impact of DW schemes on the underlying tensors can be appreciated by comparing the orientation dependence of the precision and accuracy of each contrast for a tensor with low, moderate, and high FA.

Fig. 11.

Simulated interactions of SNR, tensor orientation and DW scheme. Noise level and orientation demonstrate a differential impact on the precision and accuracy of diffusion tensor contrasts.