High resolution multidetector CT-aided tissue analysis and quantification of lung fibrosis

Abstract

Rationale and objectives: Volumetric high-resolution scans can be acquired of the lungs with multidetector CT (MDCT). Such scans have potential to facilitate useful visualization, characterization, and quantification of the extent of diffuse lung diseases, such as usual interstitial pneumonitis or idiopathic pulmonary fibrosis (UIP/IPF). There is a need to objectify, standardize, and improve the accuracy and repeatability of pulmonary disease characterization and quantification from such scans. This article presents a novel texture analysis approach toward classification and quantification of various pathologies present in lungs with UIP/IPF. The approach integrates a texture matching method with histogram feature analysis.

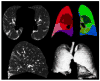
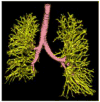
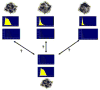
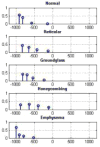
Materials and methods: Patients with moderate UIP/IPF were scanned on a Lightspeed 8-detector GE CT scanner (140 kVp, 250 mAs). Images were reconstructed with 1.25-mm slice thickness in a high-frequency sparing algorithm (BONE) with 50% overlap and a 512 x 512 axial matrix, (0.625 mm(3) voxels). Eighteen scans were used in this study. Each dataset is preprocessed and includes segmentation of the lungs and the bronchovascular trees. Two types of analysis were performed, first an analysis of independent volume of interests (VOIs) and second an analysis of whole-lung datasets. 1) Fourteen of the 18 scans were used to create a database of independent 15 x 15 x 15 cubic voxel VOIs. The VOIs were selected by experts as having greater than 70% of the defined class. The database was composed of: honeycombing (number of VOIs 337), reticular (130), ground glass (148), normal (240), and emphysema (54). This database was used to develop our algorithm. Three progressively challenging classification experiments were designed to test our algorithm. All three experiments were performed using a 10-fold cross-validation method for error estimation. Experiment 1 consisted of a two-class discrimination: normal and abnormal. Experiment 2 consisted of a four-class discrimination: normal, reticular, honeycombing, and emphysema. Experiment 3 consisted of a five-class discrimination: normal, ground glass, reticular, honeycombing, and emphysema. 2) The remaining four scans were used to further test the algorithm on new data in the context of a whole lung analysis. Each of the four datasets was manually segmented by three experts. These datasets included normal, reticular and honeycombing regions and did not include ground glass or emphysema. The accuracy of the classification algorithm was then compared with results from experts.

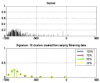
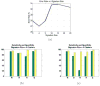
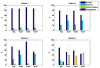
Results: Independent VOIs: 1) two-class discrimination problem (sensitivity, specificity): normal versus abnormal (92.96%, 93.78%). 2) Four-class discrimination problem: normal (92%, 95%), reticular (86%, 87%), honeycombing (74%, 98%), and emphysema (93%, 98%). 3) Five-class discrimination problem: normal (92%, 95%), ground glass (75%, 89%), reticular (22%, 92%), honeycombing (74%, 91%), and emphysema (94%, 98%). Whole-lung datasets: 1) William's index shows that algorithm classification of lungs agrees with the experts as well as the experts agree with themselves. 2) Student t-test between overlap measures of algorithm and expert (AE) and expert and expert (EE): normal (t = -1.20, P = .230), Reticular (t = -1.44, P = .155), Honeycombing (t = -3.15, P = .003). 3) Lung volumes intraclass correlation: dataset 1 (ICC = 0.9984, F = 0.0007); dataset 2 (ICC = 0.9559, F = 0); dataset 3 (ICC = 0.8623, F= 0.0015); dataset 4 (ICC = 0.7807, F = 0.0136).

Conclusions: We have demonstrated that our novel method is computationally efficient and produces results comparable to expert radiologic judgment. It is effective in the classification of normal versus abnormal tissue and performs as well as the experts in distinguishing among typical pathologies present in lungs with UIP/IPF. The continuing development of quantitative metrics will improve quantification of disease and provide objective measures of disease progression.

Fig. 1

Lung Segmentation: 1st Row: Transverse slice, Coronal slice (Peripheral and Central Regions and Lobes Outlined by color); 2nd Row: Sagittal slice, Volumetric Rendering

Fig. 2

Broncho-vascular Structure. The Bronchial tree (pink) was segmented using an algorithm involving morphological operations and region growing [21]. The Vascular tree (yellow) was segmented by thresholding the 3D line enhancement filtered image [24].

Fig. 3

The main point of the algorithm is detailed in this figure. The top three rows show the cubes of data that are known along with their histograms and canonical signatures. The bottom three rows show an unknown cube of data with its histogram and signature. The idea of the algorithm is to compare the unknown signature with the known signatures using the EMD as the metric. The unknown cube of data is assigned to the known cube's class for which the signatures are most similar.

Fig. 4

Creation of canonical signature. Top plot: Accumulated signatures from training set. Bottom plot: Canonical signatures computed by re-clustering the top plot using various amounts of training data.

Fig. 5

The canonical signatures computed for each class (Normal, Reticular, Ground glass, Honeycombing, and Emphysema) are plotted in this figure. These signatures are made up of 4 cluster centers positioned at various locations with varying frequencies. Each signature is uniquely computed for each class.

Fig. 6

Independent Volumes of Interest (VOI): transverse, coronal, sagittal Views of cubic VOIs selected within expert drawn regions. The colored cubes represent different VOIs selected within the manually traced region (red) by the expert for this particular dataset.

Fig. 7

Each column is a segmentation of a dataset by a different expert. Each row is a different orientation (transverse, coronal, and sagittal). The colors represent different tissue classes: Green-Normal and Red-Reticular.

Fig. 8

In order to determine the optimal number of clusters in a signature for a multi-class problem the error rate was measured as the number of clusters in the signature was varied. Figure (a), shows the least error with a 4 cluster signature. Figure (b), shows the sensitivity (true positive rate) in green and specificity (true negative rate) in yellow for the 4-class classification experiment of normal (N), reticular (R), honeycombing (H), and emphysema (E). Figure c, shows the sensitivity (true positive rate) in green and specificity (true negative rate) in yellow for the 5-class classification experiment of normal (N), ground glass (G), reticular (R), honeycombing (H), and emphysema (E). Note that the sensitivity for honeycombing class remains about the same for the 4 and 5 class problem. However, note that the sensitivity of the reticular class is significantly reduced in the 5 class problem - this is because of the similarity between the ground glass and reticular classes, detailed in the confusion matrices in Table 1 and Table 2

Fig. 9

The Williams Index CI for the Algorithm and the Experts for each class computed using the Jaccard Coefficient shown in (a). and the Volume Similarity Metric shown in (b). The Williams index tests the ability of an isolated rater to agree with the group as much as the members of the group agree amongst themselves. An upper limit of the confidence interval greater than or equal to one is indicative agreement. The metric used to measure agreement makes a difference.

Fig. 10

Classified Lungs by Algorithm and Experts. Rows 1-4 depict a transverse slice of Datasets 1-4. Column 1 is the original slice, Column 2 is the Algorithm's classification and Columns 3-5 are the Experts' 1-3 segmentation. Purple is Normal, Red is Reticular, Green is Honeycombing, Yellow is Vessel, and Blue is Airway

Fig. 11

Volumetric rendering of a classified lung. Purple is Normal, Red is Reticular, Green is Honeycombing, Yellow is Vessel, and Blue is Airway

Fig. 12

Lung Volumes calculated by Algorithm and Experts. Dataset 1, ICC = 0.9984; Dataset 2, ICC = 0.9559; Dataset 3, ICC = 0.8623; Dataset 4, ICC = 0.7807