An oscillatory interference model of grid cell firing
- PMID: 17598147
- PMCID: PMC2678278
- DOI: 10.1002/hipo.20327
An oscillatory interference model of grid cell firing
Abstract
We expand upon our proposal that the oscillatory interference mechanism proposed for the phase precession effect in place cells underlies the grid-like firing pattern of dorsomedial entorhinal grid cells (O'Keefe and Burgess (2005) Hippocampus 15:853-866). The original one-dimensional interference model is generalized to an appropriate two-dimensional mechanism. Specifically, dendritic subunits of layer II medial entorhinal stellate cells provide multiple linear interference patterns along different directions, with their product determining the firing of the cell. Connection of appropriate speed- and direction-dependent inputs onto dendritic subunits could result from an unsupervised learning rule which maximizes postsynaptic firing (e.g. competitive learning). These inputs cause the intrinsic oscillation of subunit membrane potential to increase above theta frequency by an amount proportional to the animal's speed of running in the "preferred" direction. The phase difference between this oscillation and a somatic input at theta-frequency essentially integrates velocity so that the interference of the two oscillations reflects distance traveled in the preferred direction. The overall grid pattern is maintained in environmental location by phase reset of the grid cell by place cells receiving sensory input from the environment, and environmental boundaries in particular. We also outline possible variations on the basic model, including the generation of grid-like firing via the interaction of multiple cells rather than via multiple dendritic subunits. Predictions of the interference model are given for the frequency composition of EEG power spectra and temporal autocorrelograms of grid cell firing as functions of the speed and direction of running and the novelty of the environment.
(c) 2007 Wiley-Liss, Inc.
Figures


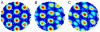
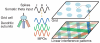

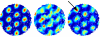
References
-
- Alonso A, Klink R. Differential electroresponsiveness of stellate and pyramidal-like cells of medial entorhinal cortex layer II. J.Neurophysiol. 1993;70:128–143. - PubMed
-
- Alonso A, Llinas RR. Subthreshold Na+-dependent theta-like rhythmicity in stellate cells of entorhinal cortex layer II. Nature. 1989;342:175–177. - PubMed
-
- Amaral DG, Witter MP. The Hippocampus. In: Paxinos G, editor. The Rat Nervous System. 2nd ed. Academic Press; New York: 1995. pp. 443–493.
-
- Barry C, Hayman R, Burgess N, Jeffery KJ. Experience-dependent rescaling of entorhinal grids. 2007 Submitted. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

