The durability of public goods changes the dynamics and nature of social dilemmas
- PMID: 17611625
- PMCID: PMC1899228
- DOI: 10.1371/journal.pone.0000593
The durability of public goods changes the dynamics and nature of social dilemmas
Abstract
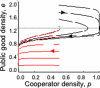
An implicit assumption underpins basic models of the evolution of cooperation, mutualism and altruism: The benefits (or pay-offs) of cooperation and defection are defined by the current frequency or distribution of cooperators. In social dilemmas involving durable public goods (group resources that can persist in the environment-ubiquitous from microbes to humans) this assumption is violated. Here, we examine the consequences of relaxing this assumption, allowing pay-offs to depend on both current and past numbers of cooperators. We explicitly trace the dynamic of a public good created by cooperators, and define pay-offs in terms of the current public good. By raising the importance of cooperative history in determining the current fate of cooperators, durable public goods cause novel dynamics (e.g., transient increases in cooperation in Prisoner's Dilemmas, oscillations in Snowdrift Games, or shifts in invasion thresholds in Stag-hunt Games), while changes in durability can transform one game into another, by moving invasion thresholds for cooperation or conditions for coexistence with defectors. This enlarged view challenges our understanding of social cheats. For instance, groups of cooperators can do worse than groups of defectors, if they inherit fewer public goods, while a rise in defectors no longer entails a loss of social benefits, at least not in the present moment (as highlighted by concerns over environmental lags). Wherever durable public goods have yet to reach a steady state (for instance due to external perturbations), the history of cooperation will define the ongoing dynamics of cooperators.
Conflict of interest statement
Figures

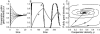
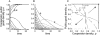
Similar articles
-
Coexistence of cooperation and defection in public goods games.Evolution. 2011 Apr;65(4):1140-8. doi: 10.1111/j.1558-5646.2010.01185.x. Epub 2010 Dec 1. Evolution. 2011. PMID: 21062277
-
Synergy and discounting of cooperation in social dilemmas.J Theor Biol. 2006 Mar 21;239(2):195-202. doi: 10.1016/j.jtbi.2005.08.040. Epub 2005 Oct 19. J Theor Biol. 2006. PMID: 16242728 Free PMC article.
-
Public goods games with reward in finite populations.J Math Biol. 2011 Jul;63(1):109-23. doi: 10.1007/s00285-010-0363-7. Epub 2010 Sep 24. J Math Biol. 2011. PMID: 20865261
-
Review: Game theory of public goods in one-shot social dilemmas without assortment.J Theor Biol. 2012 Apr 21;299:9-20. doi: 10.1016/j.jtbi.2011.06.018. Epub 2011 Jun 24. J Theor Biol. 2012. PMID: 21723299 Review.
-
A behavioral analysis of altruism.Behav Processes. 2011 May;87(1):25-33. doi: 10.1016/j.beproc.2010.12.004. Epub 2010 Dec 22. Behav Processes. 2011. PMID: 21184815 Free PMC article. Review.
Cited by
-
Live to cheat another day: bacterial dormancy facilitates the social exploitation of β-lactamases.ISME J. 2016 Mar;10(3):778-87. doi: 10.1038/ismej.2015.154. Epub 2015 Oct 27. ISME J. 2016. PMID: 26505830 Free PMC article.
-
Building the microbiome in health and disease: niche construction and social conflict in bacteria.Philos Trans R Soc Lond B Biol Sci. 2015 Aug 19;370(1675):20140298. doi: 10.1098/rstb.2014.0298. Philos Trans R Soc Lond B Biol Sci. 2015. PMID: 26150664 Free PMC article. Review.
-
Evolution of virulence: triggering host inflammation allows invading pathogens to exclude competitors.Ecol Lett. 2008 Jan;11(1):44-51. doi: 10.1111/j.1461-0248.2007.01125.x. Epub 2007 Nov 15. Ecol Lett. 2008. PMID: 18021245 Free PMC article.
-
Oligopeptide Signaling through TbGPR89 Drives Trypanosome Quorum Sensing.Cell. 2019 Jan 10;176(1-2):306-317.e16. doi: 10.1016/j.cell.2018.10.041. Epub 2018 Nov 29. Cell. 2019. PMID: 30503212 Free PMC article.
-
Equilibria and oscillations in cheat-cooperator dynamics.Evol Lett. 2023 Jul 22;7(5):339-350. doi: 10.1093/evlett/qrad032. eCollection 2023 Oct. Evol Lett. 2023. PMID: 37829502 Free PMC article.
References
-
- Hamilton WD. The genetical evolution of social behaviour. I. J Theor Biol. 1964;7:1–16. - PubMed
-
- Trivers RL. The evolution of reciprocal altruism. Q Rev Biol. 1971;46:35–57.
-
- Axelrod R. New York: Basic Books; 1984. The evolution of cooperation.
-
- Frank SA. Princeton: Priceton University Press; 1998. The foundations of Social Evolution.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

