Genetic association mapping via evolution-based clustering of haplotypes

Abstract

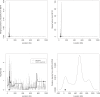
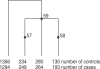
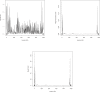
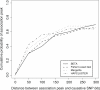
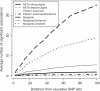
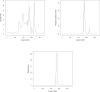
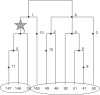
Multilocus analysis of single nucleotide polymorphism haplotypes is a promising approach to dissecting the genetic basis of complex diseases. We propose a coalescent-based model for association mapping that potentially increases the power to detect disease-susceptibility variants in genetic association studies. The approach uses Bayesian partition modelling to cluster haplotypes with similar disease risks by exploiting evolutionary information. We focus on candidate gene regions with densely spaced markers and model chromosomal segments in high linkage disequilibrium therein assuming a perfect phylogeny. To make this assumption more realistic, we split the chromosomal region of interest into sub-regions or windows of high linkage disequilibrium. The haplotype space is then partitioned into disjoint clusters, within which the phenotype-haplotype association is assumed to be the same. For example, in case-control studies, we expect chromosomal segments bearing the causal variant on a common ancestral background to be more frequent among cases than controls, giving rise to two separate haplotype clusters. The novelty of our approach arises from the fact that the distance used for clustering haplotypes has an evolutionary interpretation, as haplotypes are clustered according to the time to their most recent common ancestor. Our approach is fully Bayesian and we develop a Markov Chain Monte Carlo algorithm to sample efficiently over the space of possible partitions. We compare the proposed approach to both single-marker analyses and recently proposed multi-marker methods and show that the Bayesian partition modelling performs similarly in localizing the causal allele while yielding lower false-positive rates. Also, the method is computationally quicker than other multi-marker approaches. We present an application to real genotype data from the CYP2D6 gene region, which has a confirmed role in drug metabolism, where we succeed in mapping the location of the susceptibility variant within a small error.

Figure 1. Results from BETA, Margarita, HAPCLUSTER and Fisher's Exact Test from a Single Dataset with One Susceptibility Allele under the Default Scenario

Marginal posterior probability of association from BETA (top left), Bayes factor in favour of association at each marker from BETA (top right), p-values from Margarita and Fisher's exact test (bottom left), and posterior density of location from HAPCLUSTER (bottom right), where the dot on the x-axis indicates the position of the susceptibility mutation.

Figure 2. Perfect Phylogeny with the Highest Posterior Probability of Containing the Susceptibility Allele

At the bottom of each branch we report the case and control multiplicities of each unique haplotype in the tree.

Figure 3. Results of Fisher's Exact Test and BETA from a Single Dataset with Two Susceptibility Alleles

p-Values from Fisher's exact test for single-marker disease association (top left), the marginal posterior probability of association from BETA (top right), and the Bayes factor in favour of association at each marker from BETA (bottom centre), where the dots on the x-axis indicate the positions of two susceptibility mutations.

Figure 4. Cumulative Distribution of Distances between the Association Peak and the Causal SNP

Analysis of 50 datasets simulated under the default scenario, namely variable recombination rate, additive disease model, 1,000 cases and controls, SNP density of 1 kb, MAF of causal allele 5%, and 1.6 GRR(Aa).

Figure 5. Average Number of Significant Associations within an Interval around the Causal SNP

Analysis of 50 datasets simulated under the default scenario, namely variable recombination rate, additive disease model, 1,000 cases and controls, SNP density 1 kb, MAF of causal allele 5%, and 1.6 GRR(Aa). For “BETA strong signal” and “BETA decisive signal,” we consider markers with Bayes factors ≥10 and ≥150, respectively. For “Fisher's exact test” and “Fisher's exact test Bonferroni” we consider markers with p-values ≤0.05 and the Bonferroni-adjusted value respectively. For Margarita we consider the markerwise p-values calculated by permutation, while “Margarita Bonferroni” and “Margarita corrected” correspond to p-values corrected for multiple testing using Bonferroni and permutations, respectively.

Figure 6. Power for a Range of Models

Probability of a significant signal within 100 kb of the causal allele. Each point on the x-axis corresponds to 50 datasets under each of the simulation parameters while keeping the rest at their default values. The two points that do not belong to a line correspond to the default scenario for Margarita markerwise p-values calculated by permutation and Margarita experimentwise p-values calculated by permutation. For “BETA strong signal” and “BETA decisive signal” we consider markers with Bayes factors ≥10 and ≥150, respectively.

Figure 7. Mean False-Positive Rates (%) for Various Models

Each point on the x-axis corresponds to 50 datasets under each of the simulation parameters while keeping the rest at their default values. The three points that do not belong to a line correspond to the default scenario for Margarita markerwise p-values calculated by permutation with or without Bonferroni correction, and Margarita experimentwise p-values calculated by permutation.

Figure 8. Results of Fisher's Exact Test and BETA Using the CYP2D6 Dataset

p-Values from Fisher's exact test for single marker-disease association (top left), the marginal posterior probability of association (top right) and the Bayes factor in favour of association at each marker (bottom centre) from the CYP2D6 gene region, where the vertical line on the x-axis indicates the location of CYP2D6.

Figure 9. The Gene Tree Consistent with the Haplotypes in the Incidence Matrix of Table 6

Labels 1–12 refer to mutations S1–S12. At the bottom of each branch we report the multiplicity of each observed haplotype in the sample.

Figure 10. Posterior Density of Location of Causal Allele and 95% Credible Intervals

Credible intervals (95%) of causal location for two datasets simulated with 1.8 and 2.4 GRR(Aa) and all other simulation parameters at default values. The credible intervals are 150 kb and 15 kb wide, respectively.