Biological solutions to transport network design
- PMID: 17623638
- PMCID: PMC2288531
- DOI: 10.1098/rspb.2007.0459
Biological solutions to transport network design
Abstract
Transport networks are vital components of multicellular organisms, distributing nutrients and removing waste products. Animal and plant transport systems are branching trees whose architecture is linked to universal scaling laws in these organisms. In contrast, many fungi form reticulated mycelia via the branching and fusion of thread-like hyphae that continuously adapt to the environment. Fungal networks have evolved to explore and exploit a patchy environment, rather than ramify through a three-dimensional organism. However, there has been no explicit analysis of the network structures formed, their dynamic behaviour nor how either impact on their ecological function. Using the woodland saprotroph Phanerochaete velutina, we show that fungal networks can display both high transport capacity and robustness to damage. These properties are enhanced as the network grows, while the relative cost of building the network decreases. Thus, mycelia achieve the seemingly competing goals of efficient transport and robustness, with decreasing relative investment, by selective reinforcement and recycling of transport pathways. Fungal networks demonstrate that indeterminate, decentralized systems can yield highly adaptive networks. Understanding how these relatively simple organisms have found effective transport networks through a process of natural selection may inform the design of man-made networks.
Figures
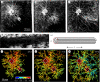

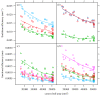
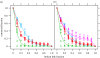
References
-
- Albert R, Barabasi A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002;74:47–97. doi:10.1103/RevModPhys.74.47 - DOI
-
- Banavar J.R, Maritan A, Rinaldo A. Size and form in efficient transportation networks. Nature. 1999;399:130–132. doi:10.1038/20144 - DOI - PubMed
-
- Banavar J.R, Damuth J, Maritan A, Rinaldo A. Supply–demand balance and metabolic scaling. Proc. Natl Acad. Sci. USA. 2002;99:10 506–10 509. doi:10.1073/pnas.162216899 - DOI - PMC - PubMed
-
- Barrat A, Barthelemy M, Pastor-Satorras R, Vespignani A. The architecture of complex weighted networks. Proc. Natl Acad. Sci. USA. 2004a;101:3747–3752. doi:10.1073/pnas.0400087101 - DOI - PMC - PubMed
-
- Barrat A, Barthelemy M, Vespignani A. Modeling the evolution of weighted networks. Phys. Rev. E. 2004b;70:066149. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

