Patterns of genetic variation in populations of infectious agents

Abstract

Background: The analysis of genetic variation in populations of infectious agents may help us understand their epidemiology and evolution. Here we study a model for assessing the levels and patterns of genetic diversity in populations of infectious agents. The population is structured into many small subpopulations, which correspond to their hosts, that are connected according to a specific type of contact network. We considered different types of networks, including fully connected networks and scale free networks, which have been considered as a model that captures some properties of real contact networks. Infectious agents transmit between hosts, through migration, where they grow and mutate until elimination by the host immune system.

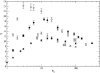
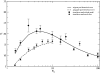
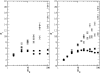
Results: We show how our model is closely related to the classical SIS model in epidemiology and find that: depending on the relation between the rate at which infectious agents are eliminated by the immune system and the within host effective population size, genetic diversity increases with R0 or peaks at intermediate R0 levels; patterns of genetic diversity in this model are in general similar to those expected under the standard neutral model, but in a scale free network and for low values of R0 a distortion in the neutral mutation frequency spectrum can be observed; highly connected hosts (hubs in the network) show patterns of diversity different from poorly connected individuals, namely higher levels of genetic variation, lower levels of genetic differentiation and larger values of Tajima's D.

Conclusion: We have found that levels of genetic variability in the population of infectious agents can be predicted by simple analytical approximations, and exhibit two distinct scenarios which are met according to the relation between the rate of drift and the rate at which infectious agents are eliminated. In one scenario the diversity is an increasing function of the level of transmission and in a second scenario it is peaked around intermediate levels of transmission. This is independent of the type of host contact structure. Furthermore for low values of R0, very heterogeneous host contact structures lead to lower levels of diversity.

Figure 1

Infected Individuals. The proportion of infected individuals, i, with increasing R₀ = N_dmK/e. Full circles are the results for scale free networks (with γ = 3) and empty circles for the island model. D = 900, N_d = 10, e = 0.01 in all network topologies. The line denotes the expected value of i under the deterministic SIS model.

Figure 2

Diversity in the metapopulation. The level of diversity π_t as a function of R₀ = N_dmK/e. The parameters values are D = 1000, N_d = 10, n_t = 50 and μ = 0.0004. The empty symbols denote the results for the island model while the full symbols correspond to scale-free networks with γ = 3. The results for e = 0.01 are represented by circles and e = 0.02 by triangles.

Figure 3

Theoretical approximations and the different topologies. Comparison of the level of diversity π_t between topologies and with the theoretical approximations. D = 900, N_d = 10, e = 0.01, n_t = 50 and μ = 0.0004 in all networks.

Figure 4

Effect of N_d in metapopulation diversity. The level of diversity, π_t, with R₀ and N_d in the island model (left panel) and scale free networks (right panel). N_d = 5 in full circles, N_d = 7 in full squares, N_d = 20 in open circles, N_d = 40 in open squares and N_d = 60 in open triangles. Other parameters are D = 1000, e = 0.05, n_t = 50 and μ = 0.0004 for all networks.

Figure 5

Frequency spectrum. The frequency spectrum of neutral mutations in scale free networks with γ = 3. In the Y-axis we plot the probability that in a sample of size n_t = 300 we find mutations with frequency k/n_t or with frequency (n_t - k)/n_t. D = 1000, N_d = 10, e = 0.01 and μ = 0.0004. Black bars correspond to R₀ = 1.5 and grey bars to R₀ = 15.

Figure 6

Level of differentiation. The level of differentiation among hosts measured as F_ST. The empty symbols denote the results for the island model, while the full symbols correspond to scale-free networks. The parameters are e = 0.01 (circles) and e = 0.02 (triangles), D = 1000, N_d = 10, n_t = 50, n_d = 5 and μ = 0.0004.

Figure 7

Within host diversity and differentiation among hosts. The level of within host diversity, π_d (in circles), and differentiation among hosts, F_ST (in triangles), as a function of connectivity k_i. The squares represent the mean values of Tajima's D within hosts, D_d. R₀ = 3 in open symbols and R₀ = 15 in filled symbols, other parameters are D = 1000, N_d = 10, e = 0.01, n_t = 50, n_d = 5 and μ = 0.0004.

Figure 8

Level of differentiation between hosts. The level of differentiation between pairs of hosts, F_ST, as a function of their topological distance (which is estimated as the minimum number of links which separates two distinct demes). A scale-free network, with γ = 3, is considered with D = 500, N_d = 10, μ = 0.0008, e = 0.01. R₀ = 3 in filled circle symbols, R₀ = 30 in empty circle symbols and R₀ = 60 in diamonds.