Sarcomere lattice geometry influences cooperative myosin binding in muscle
- PMID: 17630823
- PMCID: PMC1914368
- DOI: 10.1371/journal.pcbi.0030115
Sarcomere lattice geometry influences cooperative myosin binding in muscle
Abstract
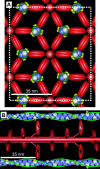
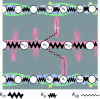
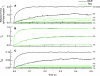
In muscle, force emerges from myosin binding with actin (forming a cross-bridge). This actomyosin binding depends upon myofilament geometry, kinetics of thin-filament Ca(2+) activation, and kinetics of cross-bridge cycling. Binding occurs within a compliant network of protein filaments where there is mechanical coupling between myosins along the thick-filament backbone and between actin monomers along the thin filament. Such mechanical coupling precludes using ordinary differential equation models when examining the effects of lattice geometry, kinetics, or compliance on force production. This study uses two stochastically driven, spatially explicit models to predict levels of cross-bridge binding, force, thin-filament Ca(2+) activation, and ATP utilization. One model incorporates the 2-to-1 ratio of thin to thick filaments of vertebrate striated muscle (multi-filament model), while the other comprises only one thick and one thin filament (two-filament model). Simulations comparing these models show that the multi-filament predictions of force, fractional cross-bridge binding, and cross-bridge turnover are more consistent with published experimental values. Furthermore, the values predicted by the multi-filament model are greater than those values predicted by the two-filament model. These increases are larger than the relative increase of potential inter-filament interactions in the multi-filament model versus the two-filament model. This amplification of coordinated cross-bridge binding and cycling indicates a mechanism of cooperativity that depends on sarcomere lattice geometry, specifically the ratio and arrangement of myofilaments.
Conflict of interest statement
Figures
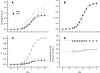
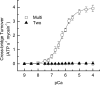


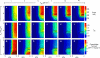
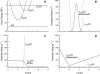
Similar articles
-
Filament compliance influences cooperative activation of thin filaments and the dynamics of force production in skeletal muscle.PLoS Comput Biol. 2012;8(5):e1002506. doi: 10.1371/journal.pcbi.1002506. Epub 2012 May 10. PLoS Comput Biol. 2012. PMID: 22589710 Free PMC article.
-
Three-dimensional stochastic model of actin-myosin binding in the sarcomere lattice.J Gen Physiol. 2016 Dec;148(6):459-488. doi: 10.1085/jgp.201611608. Epub 2016 Nov 18. J Gen Physiol. 2016. PMID: 27864330 Free PMC article.
-
Is sarcomere lattice geometry optimal? Analysis of several potential virtual polygon cross-sectional patterns for actin and myosin myofilaments in muscle.Anat Rec (Hoboken). 2014 Sep;297(9):1770-6. doi: 10.1002/ar.22971. Anat Rec (Hoboken). 2014. PMID: 25125188
-
Regulation of contraction in striated muscle.Physiol Rev. 2000 Apr;80(2):853-924. doi: 10.1152/physrev.2000.80.2.853. Physiol Rev. 2000. PMID: 10747208 Review.
-
The three filament model of skeletal muscle stability and force production.Mol Cell Biomech. 2012 Sep;9(3):175-91. Mol Cell Biomech. 2012. PMID: 23285733 Review.
Cited by
-
Force-velocity and tension transient measurements from Drosophila jump muscle reveal the necessity of both weakly-bound cross-bridges and series elasticity in models of muscle contraction.Arch Biochem Biophys. 2021 Apr 15;701:108809. doi: 10.1016/j.abb.2021.108809. Epub 2021 Feb 18. Arch Biochem Biophys. 2021. PMID: 33610561 Free PMC article.
-
Poorly understood aspects of striated muscle contraction.Biomed Res Int. 2015;2015:245154. doi: 10.1155/2015/245154. Epub 2015 Apr 16. Biomed Res Int. 2015. PMID: 25961006 Free PMC article. Review.
-
Geometrical conditions indispensable for muscle contraction.Int J Mol Sci. 2011;12(4):2138-57. doi: 10.3390/ijms12042138. Epub 2011 Mar 29. Int J Mol Sci. 2011. PMID: 21731432 Free PMC article.
-
Kinetics of cardiac myosin isoforms in mouse myocardium are affected differently by presence of myosin binding protein-C.J Muscle Res Cell Motil. 2014 Dec;35(5-6):267-78. doi: 10.1007/s10974-014-9390-0. Epub 2014 Oct 7. J Muscle Res Cell Motil. 2014. PMID: 25287107 Free PMC article.
-
Multiscale and Multiaxial Mechanics of Vascular Smooth Muscle.Biophys J. 2017 Aug 8;113(3):714-727. doi: 10.1016/j.bpj.2017.06.017. Biophys J. 2017. PMID: 28793225 Free PMC article.
References
-
- Huxley AF. Muscle structure and theories of contraction. Prog Biophys Biophys Chem. 1957;7:255–318. - PubMed
-
- Lymn RW, Taylor EW. Mechanism of adenosine triphosphate hydrolysis by actomyosin. Biochemistry. 1971;10:4617–4624. - PubMed
-
- Pate E, Cooke R. A model of crossbridge action: The effects of ATP, ADP, and Pi . J Muscle Res Cell Motil. 1989;10:181–196. - PubMed
-
- Tobacman LS. Thin filament-mediated regulation of cardiac contraction. Ann Rev Physiol. 1996;58:447–481. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

