Optimal timing and duration of induction therapy for HIV-1 infection
- PMID: 17630827
- PMCID: PMC1914372
- DOI: 10.1371/journal.pcbi.0030133
Optimal timing and duration of induction therapy for HIV-1 infection
Abstract
The tradeoff between the need to suppress drug-resistant viruses and the problem of treatment toxicity has led to the development of various drug-sparing HIV-1 treatment strategies. Here we use a stochastic simulation model for viral dynamics to investigate how the timing and duration of the induction phase of induction-maintenance therapies might be optimized. Our model suggests that under a variety of biologically plausible conditions, 6-10 mo of induction therapy are needed to achieve durable suppression and maximize the probability of eradicating viruses resistant to the maintenance regimen. For induction regimens of more limited duration, a delayed-induction or -intensification period initiated sometime after the start of maintenance therapy appears to be optimal. The optimal delay length depends on the fitness of resistant viruses and the rate at which target-cell populations recover after therapy is initiated. These observations have implications for both the timing and the kinds of drugs selected for induction-maintenance and therapy-intensification strategies.
Conflict of interest statement
Figures
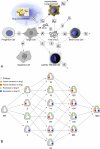


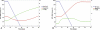
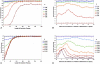
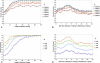
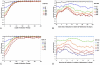
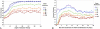
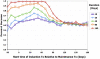
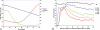
References
-
- Yeni PG, Hammer SM, Hirsch MS, Saag MS, Schechter M, et al. Treatment for adult HIV infection: 2004 recommendations of the International AIDS Society—USA Panel. JAMA. 2004;292:251–265. - PubMed
-
- Saag MS. Initiation of antiretroviral therapy: Implications of recent findings. Top HIV Med. 2004;12:83–88. - PubMed
-
- Raguin G, Chene G, Morand-Joubert L, Taburet AM, Droz C, et al. Salvage therapy with amprenavir, lopinavir and ritonavir 200 mg/d or 400 mg/d in HIV-infected patients in virological failure. Antivir Ther. 2004;9:615–625. - PubMed
-
- Murphy MD, Marousek GI, Chou S. HIV protease mutations associated with amprenavir resistance during salvage therapy: Importance of I54M. J Clin Virol. 2004;30:62–67. - PubMed
-
- Fournier S, Chaffaut C, Maillard A, Loze B, Lascoux C, et al. Factors associated with virological response in HIV-infected patients failing antiretroviral therapy: A prospective cohort study. HIV Med. 2005;6:129–134. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

