A first-principles model of early evolution: emergence of gene families, species, and preferred protein folds

Abstract

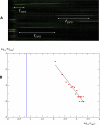
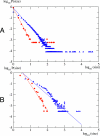
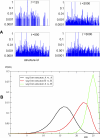
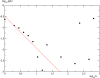
In this work we develop a microscopic physical model of early evolution where phenotype--organism life expectancy--is directly related to genotype--the stability of its proteins in their native conformations-which can be determined exactly in the model. Simulating the model on a computer, we consistently observe the "Big Bang" scenario whereby exponential population growth ensues as soon as favorable sequence-structure combinations (precursors of stable proteins) are discovered. Upon that, random diversity of the structural space abruptly collapses into a small set of preferred proteins. We observe that protein folds remain stable and abundant in the population at timescales much greater than mutation or organism lifetime, and the distribution of the lifetimes of dominant folds in a population approximately follows a power law. The separation of evolutionary timescales between discovery of new folds and generation of new sequences gives rise to emergence of protein families and superfamilies whose sizes are power-law distributed, closely matching the same distributions for real proteins. On the population level we observe emergence of species--subpopulations that carry similar genomes. Further, we present a simple theory that relates stability of evolving proteins to the sizes of emerging genomes. Together, these results provide a microscopic first-principles picture of how first-gene families developed in the course of early evolution.

Figure 1. Schematic Representation of the Genome and Population Dynamics in the Model

Individual genes undergo mutations and duplications. Organisms as a whole can replicate, passing their genomes to the progeny, or die, effectively discarding the genome.

Figure 2. Time Progression of an Evolution Run

(A) Structural repertoire of an exponentially growing population as a function of time (abscissa) is shown. Ordinate represents the sequential number of the structure out of the 103,346 possibles, and abundance of a structure at a given time is encoded by color. Bright green, abundant structures; black, rare or nonexistent structures. Arrows point to the discoveries of DPSs (bright lines in the structure repertoire). (B) Population as a function of time is presented. Exponential growth sets in as soon as stable DPSs have been found. (C) Shown is mean native state probability P _nat, an equivalent of mean population fitness as a function of time.

Figure 3. Distribution of Life Times of DPSs

(A) Lifetimes are defined as a span between the emergence of a DPS when it takes over at least 20% of the gene population (bright line) until its extinction as a DPS when it no longer dominates the population. (B) The lifetime distribution of DPSs approximately follows a power law with exponent 1.87. DPS folds persist over many generations and eventually give rise to protein superfamilies. Blue line, mean lifetime of an organism.

Figure 4. Distributions of Protein Family and Superfamily Sizes in Model Evolution and in Reality

Distribution of family and superfamily sizes (A) model evolution. Blue triangles represent the number of sequences folding into the same structure (gene family); the blue solid line approximates a power law with exponent −1.77. Red circles, distribution of the number of nonhomologous (Hamming distance >56%) sequences folding into the same structure (superfamilies); red solid line, a power law with exponent −2.92. (B) Orthologous gene family and superfamily sizes in real proteins are shown. Red circles, the number of different functions performed by each domain as defined by InterPro (Bin size = 2 and Pearson R = 0.97 of fit with slope = −2.2); blue triangles, the number of nonredundant sequences folding into each domain. (Bin size = 10 and Pearson R = 0.92 of fit with slope = −1.5.)

Figure 5. Analytic Prediction for the Maximum Number of Genes in an Organism as Function of the Mean Protein Stability P _nat (f in Equation 2) in the Analytical Model and the Results of Simulations

The data from 50 simulation runs, both exponentially growing and extinct, have been combined. Red curve, analytical model; black dots, results of the simulations.

Figure 6. Emergence of Species

(A) Structural repertoire of an evolution run developing two DPSs is shown. The height of the bars represents the number of sequences folding into a given structure; the structure numbers are arbitrary. (B) Histograms of pairwise Hamming distances between sequences corresponding to the two DPSs (black and red curves) demonstrate sequence similarity within the structure's superfamily. The histogram of Hamming distances between the sequences folding into one DPS and the sequences folding into another DPS (green) shows a lack of sequence similarity. As each organism bears only one of the two DPSs, one can say that this evolution run resulted in the formation of two different strains or species of organisms.

Figure 7. Degree Distribution of Structure Similarity Graph (PDUG) of the Surviving Populations in the Evolution Model

The similarity threshold was set to Q = 17, corresponding to the transition point in the largest cluster size (the giant component) of the graph. The slope of the linear approximation is −1.4 for log k < 1.75.

Figure 8. Schematic Representation of the Formation of Protein Folds and Superfamilies by Punctuated Jumps in the Divergent Model

Invention of new folds and their spread in population is a rare event of which the timescale exceeds the lifetime of organisms and the mutation timescale. On a shorter timescale, mutations that do not change protein structure significantly occur and fix in the population, which gives rise to protein families (on the shortest timescales) or superfamilies (on timescales longer than mutational but shorter than fold innovation). Evolutionary time increases from left to right.

Figure 9. Node Degree Correlations in Evolved and Natural PDUG

(A) Shown is the Z score for the probability P(k ₁,k ₂) of the two nodes with degree k₁,k₂ being connected to each other in the natural PDUG. Unlike in other networks, nodes of similar degree tend to be connected. (B) The Z score plot of P(k ₁,k ₂) for the structure similarity graph obtained in the evolution model is remarkably similar to the actual one.