Parameter estimation and prediction for the course of a single epidemic outbreak of a plant disease

Abstract

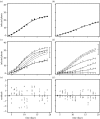
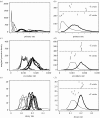
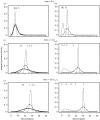
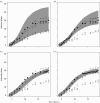
Many epidemics of plant diseases are characterized by large variability among individual outbreaks. However, individual epidemics often follow a well-defined trajectory which is much more predictable in the short term than the ensemble (collection) of potential epidemics. In this paper, we introduce a modelling framework that allows us to deal with individual replicated outbreaks, based upon a Bayesian hierarchical analysis. Information about 'similar' replicate epidemics can be incorporated into a hierarchical model, allowing both ensemble and individual parameters to be estimated. The model is used to analyse the data from a replicated experiment involving spread of Rhizoctonia solani on radish in the presence or absence of a biocontrol agent, Trichoderma viride. The rate of primary (soil-to-plant) infection is found to be the most variable factor determining the final size of epidemics. Breakdown of biological control in some replicates results in high levels of primary infection and increased variability. The model can be used to predict new outbreaks of disease based upon knowledge from a 'library' of previous epidemics and partial information about the current outbreak. We show that forecasting improves significantly with knowledge about the history of a particular epidemic, whereas the precision of hindcasting to identify the past course of the epidemic is largely independent of detailed knowledge of the epidemic trajectory. The results have important consequences for parameter estimation, inference and prediction for emerging epidemic outbreaks.

Figure 1

Disease progress curves and residuals for damping-off of radish plants caused by R. solani in the absence (a,c,e) and in the presence (b,d,f) of the biocontrol agent, T. viride (Kleczkowski et al. 1996). (a,b) The average behaviour; circles represent observed data and lines the fit based upon the model of Kleczkowski et al. (1996), fitted to averaged replicate data. (c,d) The results of fitting model (2.2) to individual replicates, with solid lines representing the median of the simulated marginal posterior distribution of y_i(t_j). Broken lines show boundaries of the 95% high-density region based upon the normal approximation and for clarity are shown for replicate 1 only. Error bars show the maximum extent of the within-replicate variability assumed by the binomial model, for replicate 1 only. (e,f) Residuals for the fit in (c,d), respectively. In (c)–(f), data points are labelled 1–5 to indicate which replicate epidemic they represent. (This labelling is consistent across all subsequent figures.)

Figure 2

Marginal posterior densities for individual replicate parameters θ⁽ⁱ⁾ (a,c,e) and for population parameters μ (b,d,f), in the absence (thick line) and in the presence (thin line) of T. viride. In (b,d,f), labelled points represent modes of marginal posterior densities for individual replicate parameters θ⁽ⁱ⁾, while labels 1–5 indicate which replicate epidemic they represent. For ease of viewing, the labels are arbitrarily distributed vertically and separated by a dashed line. (a,b) Primary infection rate, r_p; (c,d) secondary infection rate, r_s; (e,f) decay rate, a.

Figure 3

Marginal posterior distributions for disease levels in the absence (a,c,e) and in the presence (b,d,f) of the biocontrol agent. Solid lines represent predictions for the population behaviour (between-replicate variability), whereas broken lines show predictions for one of the replicates (K₁=1; within-replicate variability) based upon the normal distribution model for $\text{Pr}({\mathit{y}}^{(i)}|{\mathit{\theta }}^{(i)})$. Points show the extent of the within-replicate variability for the binomial model. Labels 1–5 represent replicated data to indicate which replicate epidemic they represent.

Figure 4

Forecasting and hindcasting individual outbreaks. (a,b) show 95% highest predictive density regions (HPDRs) for forecasting one of the replicate epidemics from figure 1 (K₁=4). The thick line represents the ‘known’ part of the trajectory, whereas filled circles show the actual ‘future’ (or ‘past’) outbreak. Forecasting is based on (a) three (4–6 d) or (b) six (4–9 d) initial days of data. Hindcasting in (c,d) estimates the outbreak levels in the past based upon the last (c) three (17–19 d) or (d) six (13–19 d) data points. Open circles show replicates used as a library. The width of the HPDR at t=19 d (for forecasting) and 8 d (for hindcasting) is subsequently used to characterize predictability for individual replicates (figure 5). Broken lines show the median of the predictive posterior density.

Figure 5

Forecasting and hindcasting individual outbreaks. (a,b) The width of the 95% highest predictive density regions (HPDRs) for forecasting final levels (t=19 d) of replicate epidemics. (c,d) The width of the 95% high-density regions for hindcasting the disease levels at t=8 d. Cut-off time for forecasting is the date for the last measurement, whereas for hindcasting it is the earliest date for which data are assumed to exist. Plots (a,c) correspond to the case without and (b,d) with the biocontrol agent.