Numerical modelling of label-structured cell population growth using CFSE distribution data

Abstract

Background: The flow cytometry analysis of CFSE-labelled cells is currently one of the most informative experimental techniques for studying cell proliferation in immunology. The quantitative interpretation and understanding of such heterogenous cell population data requires the development of distributed parameter mathematical models and computational techniques for data assimilation.

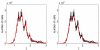
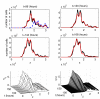
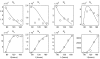
Methods and results: The mathematical modelling of label-structured cell population dynamics leads to a hyperbolic partial differential equation in one space variable. The model contains fundamental parameters of cell turnover and label dilution that need to be estimated from the flow cytometry data on the kinetics of the CFSE label distribution. To this end a maximum likelihood approach is used. The Lax-Wendroff method is used to solve the corresponding initial-boundary value problem for the model equation. By fitting two original experimental data sets with the model we show its biological consistency and potential for quantitative characterization of the cell division and death rates, treated as continuous functions of the CFSE expression level.

Conclusion: Once the initial distribution of the proliferating cell population with respect to the CFSE intensity is given, the distributed parameter modelling allows one to work directly with the histograms of the CFSE fluorescence without the need to specify the marker ranges. The label-structured model and the elaborated computational approach establish a quantitative basis for more informative interpretation of the flow cytometry CFSE systems.

Figure 1

CFSE dilution (left) and typical CFSE intensity histograms (right).

Figure 2

The original CFSE histograms at days 0,1,2,4,5 (data set 2).

Figure 3

The performance of the smoothing procedure for CFSE intensity histograms. The original CFSE histogram (black curve) and two smoothed histograms (red curves) obtained by the algorithm in [26] using the smoothing factor (6) with q = 0.03 (left) and q = 0.05 (right).

Figure 4

Propagation of the discontinuities of the solution to model (4) and the effect of the mesh refinement and the filtering procedure. Left: Solution n(t, z) of model (4) for t = 120 (hours) with the best-fit parameters estimated for data set 2. Dashed lines indicate positions of the discontinuities of the exact solution: zj∗ MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacH8akY=wiFfYdH8Gipec8Eeeu0xXdbba9frFj0=OqFfea0dXdd9vqai=hGuQ8kuc9pgc9s8qqaq=dirpe0xb9q8qiLsFr0=vr0=vr0dc8meaabaqaciaacaGaaeqabaqabeGadaaakeaacqWG6bGEdaqhaaWcbaGaemOAaOgabaGaey4fIOcaaaaa@30A2@ = z0∗ MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacH8akY=wiFfYdH8Gipec8Eeeu0xXdbba9frFj0=OqFfea0dXdd9vqai=hGuQ8kuc9pgc9s8qqaq=dirpe0xb9q8qiLsFr0=vr0=vr0dc8meaabaqaciaacaGaaeqabaqabeGadaaakeaacqWG6bGEdaqhaaWcbaGaeGimaadabaGaey4fIOcaaaaa@3033@ - j log₁₀ γ, j = 0, 1, ..., 10, z0∗ MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacH8akY=wiFfYdH8Gipec8Eeeu0xXdbba9frFj0=OqFfea0dXdd9vqai=hGuQ8kuc9pgc9s8qqaq=dirpe0xb9q8qiLsFr0=vr0=vr0dc8meaabaqaciaacaGaaeqabaqabeGadaaakeaacqWG6bGEdaqhaaWcbaGaeGimaadabaGaey4fIOcaaaaa@3033@ ≈ 2.58, γ ≈ 1.71. Right (top): The effect of the mesh refinement on the computed solution in a neighborhood of the discontinuity at z ≈ 2.347. Dashed, solid and dot-dashed curves indicate the solution computed using the mesh size N = 500, 1000, 2000, respectively. Right (bottom): The effect of the filtering procedure: the solution computed with and without the filtering (dashed, respectively solid curves). N = 1000.

Figure 5

The experimental data set 1 and the model solution corresponding to the best-fit parameter estimates. Two first rows: Experimental data (black curves) and the best-fit solution of model (4) (red curves). The initial function is shown by a blue dashed curve. The last row presents the cell population surface: experimental data (left) and the model solution (right) as functions of time and the log₁₀-transform of the marker expression level.

Figure 6

For data set 1: the estimated rate functions and parameters of PDE model (4) and ODE model (15) and the kinetics of the total number of live lymphocytes predicted by both models. Left: Dependence of the estimated turnover functions α(z) and β(z⁾ on the log₁₀-transformed marker intensity. The best-fit estimates a_k, k = 1, ..., 21, are indicated by circles. Stars specify the best-fit estimates for the birth and death parameters α_j, β_j, j = 0, ..., 5, of the ODE model (15). They are placed in the middle of the CFSE intervals which correspond to subsequent division numbers starting from 0. Right: The kinetics of the total number of live lymphocytes for data set 1 (circle) predicted by the PDE and ODE models (solid and dashed curves, respectively).

Figure 7

The experimental data set 2 and the model solution corresponding to the best-fit parameter estimates. Two first rows: Experimental data (black curves) and the best-fit solution of model (4) (red curves). The initial function is shown by a blue dashed curve. The last row presents the cell population surface: experimental data (left) and the model solution (right) as functions of time and the log₁₀-transform of the marker expression level.

Figure 8

For data set 2: the estimated rate functions and parameters of PDE model (4) and ODE model (15) and the kinetics of the total number of live lymphocytes predicted by both models. Left: Dependence of the estimated cell turnover functions α(z) and β(z) on the log₁₀-transformed marker intensity. The best-fit estimates a_k, b_k, k = 1, ..., 22, are indicated by circles. Stars specify the best-fit estimates for the birth and death parameters α_j, β_j, j = 0, ..., 5, of the ODE model (15). They are placed in the middle of the CFSE intervals which correspond to subsequent division numbers starting from 0. Right: The kinetics of the total number of live lymphocytes for data set 2 (circle) predicted by the PDE and ODE models (solid and dashed curves, respectively).

Figure 9

Experimental data set 1 and the best-fit solution of the compartmental ODE model. Experimental data are denoted by circles, the best-fit solution is denoted by solid lines. N_j is the number of cells divided j times.

Figure 10

Experimental data set 2 and the best-fit solution of the compartmental ODE model. Experimental data are denoted by circles, the best-fit solution is denoted by solid lines. N_j is the number of cells divided j times.