Cell force microscopy on elastic layers of finite thickness

Abstract

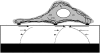
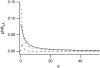
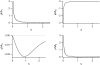
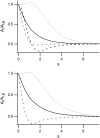
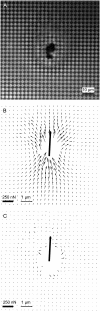
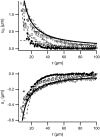
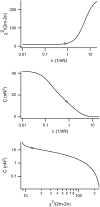
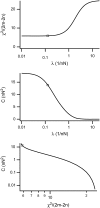
Forces applied by cells to substrates can be measured using soft substrates with embedded displacement markers. Traction forces are retrieved from microscopic images by determining the displacements of these markers and fitting the generating forces. Here we show that using elastic films of 5-10-microm thickness one can improve the spatial resolution of the technique. To this end we derived explicit equations for the mechanical response of an elastic layer of finite thickness to point forces. Moreover, these equations allow highly accurate force measurements on eukaryotic cells on films where finite thickness effects are relevant (below approximately 60 microm).

FIGURE 1

The basic principle of traction force microscopy. A cell (gray) adheres to an elastic substrate predominantly at specific locations (black ellipses). Mechanical forces (solid arrows) result in deformations of the substrate (dotted arrows) that decay in normal direction (dotted lines) and in tangential direction (not shown). The elastic film is supported by a rigid substrate, in general a microscope coverslip (black).

FIGURE 2

The deviatory part of the solutions, A_{i, A}; cf. Eqs. 5 and 7–11. The Poisson's number, σ, is 1/2. (Solid line) A_{1, A}; (dotted line) A_{2, A}; (dashed line) A_{3, A}; and (dash-dotted line) A_{4, A}.

FIGURE 3

The functions A_i from Eq. 4 for Poisson's number σ = 1/2. The dotted lines denote the Boussinesq solutions, i.e., the solutions for an infinitely thick substrate. Note the different scale for A₃.

FIGURE 4

The ratios between the finite layer solutions, A_i, and the Boussinesq solutions, A_{i, B}. (Solid line) A₁/A_{1, B}; (dotted line) A₂/A_{2, B}; (dashed line) A₃/A_{3, B}; and (dash-dotted line) A₄/A_{4, B}. (Top), σ = 0.3; (bottom) σ = 0.5; here A_{3, B} = 0 therefore only three curves are shown.

FIGURE 5

Needle deformation test of a 17-μm-thick layer of cross-linked PDMS. (A) A micrograph of the sample before deformation. The lattice constant of the microstructure is 3.5 μm. (B) The corresponding displacement field. The fat arrow denotes the force applied by the pipette (500 nN), the thin arrows the displacements of the dots. Please note the different scalings of space and displacement. (C) The deviations between the measured displacements and the ones calculated from the fitted point force.

FIGURE 6

Deformation fields of elastomer films along lines inclined by 45° to the force. Shown are the displacements of all points of the microstructure along a 7-μm-wide corridor centered around these diagonals. Layer thicknesses are 8 μm (•), 17 μm (□), 54 μm (▵), 84 μm (∇), and 126 μm (+). All deformations were scaled to the mean of the generating forces (0.66 μN), the scaling factors ranged from 0.59 to 1.66. (Top) The displacement components along the force direction. (Bottom) The displacement components perpendicular to the force direction. In both figures the displacements due to a point force as calculated by the finite layer theory are shown as dashed lines for the two lowest thicknesses. Moreover, the bold lines denote the results of the Boussinesq theory.

FIGURE 7

A cardiac fibroblast on thin elastic substrate (6.6 μm). (A) Reflection image (RICM) of the cell and bead displacements (white arrows). Note the different scaling of distances and displacements. (B) Forces calculated with the finite layer theory. (C) Forces evaluated assuming infinite layer thickness.

FIGURE 8

A cardiac fibroblast on a 79-μm-thick elastomer film. (Top) Reflection image (RICM) of cell and bead displacements (white arrows). (Bottom) Forces.

FIGURE 9

Results of the regularized least squares fit algorithm for a cell on a thick elastic substrate (79 μm; same data as in Fig. 8). See Eq. 2 for definitions of the terms. (Top) The sum of the squared deviations of the displacement field normalized by the degrees of freedom of the fit 2(m − n). (Middle) The constraint C, i.e., the sum of the squared forces. (Bottom) Variation of C with the normalized χ². Open boxes denote the regularization parameter chosen for force retrieval.

FIGURE 10

Results of the regularized least squares fit algorithm for a cell on a thin elastic substrate (6.6 μm; same data as in Fig. 7 B). See Eq. 2 for definitions of the terms. (Top) The sum of the squared deviations of the displacement field normalized by the degrees of freedom of the fit 2(m − n). (Middle) The constraint C, i.e., the sum of the squared forces. (Bottom) Variation of C with the normalized χ². Open boxes denote the regularization parameter chosen for force retrieval.

FIGURE 11

Divergences of normalized deformation fields caused by cells. (Top) Film thickness 9.5 μm; (bottom) film thickness 97 μm. Note the different gray scales: (top) from −0.09 1/μm to 0.09 1/μm; (bottom) from −0.02 1/μm to 0.02 1/μm.

FIGURE 12

Simulated deformation fields. (A) The geometry. Forces were applied uniformly over ellipses with 5 μm length and 2 μm width that were equally distributed over the short sides of a 70 × 35 μm sized rectangle. Forces were alternated between 50 and 150 nN. (B) Film thickness 4.5 μm. Resulting deformation field (green arrows) and retrieved forces assuming the correct thickness (red arrows) or infinite layer thickness (black arrows with gray borders). (C) Layer thickness 100 μm. Here forces for correct thickness and infinite thickness coincide. For clarity only 50% of the used displacements are shown in panels B and C.