Modelling the spatial dynamics of plasmid transfer and persistence
- PMID: 17660444
- PMCID: PMC2613009
- DOI: 10.1099/mic.0.2006/004531-0
Modelling the spatial dynamics of plasmid transfer and persistence
Abstract
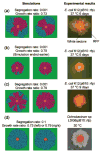
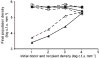
Bacterial plasmids are extra-chromosomal genetic elements that code for a wide variety of phenotypes in their bacterial hosts and are maintained in bacterial communities through both vertical and horizontal transfer. Current mathematical models of plasmid-bacteria dynamics, based almost exclusively on mass-action differential equations that describe these interactions in completely mixed environments, fail to adequately explain phenomena such as the long-term persistence of plasmids in natural and clinical bacterial communities. This failure is, at least in part, due to the absence of any spatial structure in these models, whereas most bacterial populations are spatially structured in microcolonies and biofilms. To help bridge the gap between theoretical predictions and observed patterns of plasmid spread and persistence, an individual-based lattice model (interacting particle system) that provides a predictive framework for understanding the dynamics of plasmid-bacteria interactions in spatially structured populations is presented here. To assess the accuracy and flexibility of the model, a series of experiments that monitored plasmid loss and horizontal transfer of the IncP-1beta plasmid pB10 : : rfp in Escherichia coli K12 and other bacterial populations grown on agar surfaces were performed. The model-based visual patterns of plasmid loss and spread, as well as quantitative predictions of the effects of different initial parental strain densities and incubation time on densities of transconjugants formed on a 2D grid, were in agreement with this and previously published empirical data. These results include features of spatially structured populations that are not predicted by mass-action differential equation models.
Figures

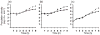
Similar articles
-
Spatial structure and nutrients promote invasion of IncP-1 plasmids in bacterial populations.ISME J. 2008 Oct;2(10):1024-39. doi: 10.1038/ismej.2008.53. Epub 2008 Jun 5. ISME J. 2008. PMID: 18528415 Free PMC article.
-
On the meaning and estimation of plasmid transfer rates for surface-associated and well-mixed bacterial populations.J Theor Biol. 2012 Feb 7;294:144-52. doi: 10.1016/j.jtbi.2011.10.034. Epub 2011 Nov 9. J Theor Biol. 2012. PMID: 22085738 Free PMC article.
-
The population biology of bacterial plasmids: a hidden Markov model approach.Genetics. 2007 Jun;176(2):957-68. doi: 10.1534/genetics.106.061937. Epub 2006 Dec 6. Genetics. 2007. PMID: 17151258 Free PMC article.
-
Plasmid persistence: costs, benefits, and the plasmid paradox.Can J Microbiol. 2018 May;64(5):293-304. doi: 10.1139/cjm-2017-0609. Epub 2018 Mar 21. Can J Microbiol. 2018. PMID: 29562144 Review.
-
Demonstrating plasmid-based horizontal gene transfer in complex environmental matrices: a practical approach for a critical review.Sci Total Environ. 2014 Sep 15;493:872-82. doi: 10.1016/j.scitotenv.2014.06.070. Epub 2014 Jul 5. Sci Total Environ. 2014. PMID: 25000583 Review.
Cited by
-
Microbial herd protection mediated by antagonistic interaction in polymicrobial communities.Appl Environ Microbiol. 2016 Dec;82(23):6881-6888. doi: 10.1128/AEM.02210-16. Epub 2016 Sep 16. Appl Environ Microbiol. 2016. PMID: 27637882 Free PMC article.
-
Tunable recombinant protein expression in E. coli: enabler for continuous processing?Appl Microbiol Biotechnol. 2016 Jul;100(13):5719-28. doi: 10.1007/s00253-016-7550-4. Epub 2016 May 12. Appl Microbiol Biotechnol. 2016. PMID: 27170324 Free PMC article. Review.
-
Harmful behaviour through plasmid transfer: a successful evolutionary strategy of bacteria harbouring conjugative plasmids.Philos Trans R Soc Lond B Biol Sci. 2022 Jan 17;377(1842):20200473. doi: 10.1098/rstb.2020.0473. Epub 2021 Nov 29. Philos Trans R Soc Lond B Biol Sci. 2022. PMID: 34839709 Free PMC article.
-
In situ monitoring of IncF plasmid transfer on semi-solid agar surfaces reveals a limited invasion of plasmids in recipient colonies.Plasmid. 2012 Mar;67(2):155-61. doi: 10.1016/j.plasmid.2012.01.001. Epub 2012 Jan 10. Plasmid. 2012. PMID: 22248925 Free PMC article.
-
Origin-of-transfer sequences facilitate mobilisation of non-conjugative antimicrobial-resistance plasmids in Staphylococcus aureus.Nucleic Acids Res. 2015 Sep 18;43(16):7971-83. doi: 10.1093/nar/gkv755. Epub 2015 Aug 3. Nucleic Acids Res. 2015. PMID: 26243776 Free PMC article.
References
-
- Beaudoin DL, Bryers JD, Cunningham AB, Peretti SW. Mobilization of broad host range plasmid from Pseudomonas putida to established biofilm of Bacillus azotoformans. II. Modeling. Biotechnol Bioeng. 1998;57:280–286. - PubMed
-
- Beloin C, Valle J, Latour-Lambert P, Faure P, Kzreminski M, Balestrino D, Haagensen JA, Molin S, Prensier G, et al. Global impact of mature biofilm lifestyle on Escherichia coli K-12 gene expression. Mol Microbiol. 2004;51:659–674. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Molecular Biology Databases
Miscellaneous

