Empirical Bayes inference of pairwise F(ST) and its distribution in the genome

Abstract

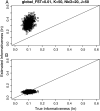
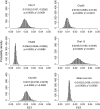
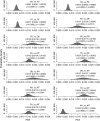
Populations often have very complex hierarchical structure. Therefore, it is crucial in genetic monitoring and conservation biology to have a reliable estimate of the pattern of population subdivision. F(ST)'s for pairs of sampled localities or subpopulations are crucial statistics for the exploratory analysis of population structures, such as cluster analysis and multidimensional scaling. However, the estimation of F(ST) is not precise enough to reliably estimate the population structure and the extent of heterogeneity. This article proposes an empirical Bayes procedure to estimate locus-specific pairwise F(ST)'s. The posterior mean of the pairwise F(ST) can be interpreted as a shrinkage estimator, which reduces the variance of conventional estimators largely at the expense of a small bias. The global F(ST) of a population generally varies among loci in the genome. Our maximum-likelihood estimates of global F(ST)'s can be used as sufficient statistics to estimate the distribution of F(ST) in the genome. We demonstrate the efficacy and robustness of our model by simulation and by an analysis of the microsatellite allele frequencies of the Pacific herring. The heterogeneity of the global F(ST) in the genome is discussed on the basis of the estimated distribution of the global F(ST) for the herring and examples of human single nucleotide polymorphisms (SNPs).

Figure 1.—

The conventional G_ST (A) and empirical Bayes (B) estimates of pairwise from 1000 simulations under the infinite-island model at various levels of (0.01, 0.05, 0.1, 0.2) over subpopulations. The mean allele frequencies assumed were with J = 50. The number of sampling localities (K) was set at 50. The sample size N_k/2 (individuals) was common to all localities and was set at 20 individuals.

Figure 2.—

The conventional informativeness of assignment I_n (Rosenberg et al. 2003) (A) and empirical Bayes (B) estimates of I_n from 1000 simulations for the case of The mean allele frequencies assumed were with J = 50. The number of sampling localities (K) was set at 50 and the sample size N_k/2 (individuals) was common to all localities and was set at 20 individuals.

Figure 3.—

Mean (top left) and root relative mean squared error (top right) of the conventional G_ST (red circle) and empirical Bayes estimators (blue circle) of pairwise from 1000 simulations under the stepping-stone models. Means and root MSEs were plotted on the true 's which fluctuated very slightly when small uniform random variables were added to prevent the points overlapping heavily. The number of subpopulations (K) was set at 15 and the pairwise between two adjacent populations was set at 0.001 (case 1) and 0.0005 (case 2). The sample size N_k/2 (individuals) was common to all localities and set at 20 individuals. Only the results for case 1 are shown. The results of the MDS analysis of two data sets are given in the bottom section; black circles show the true population structure, and the estimated population structure based on the conventional (red “*”) and empirical Bayes estimates (blue “+”) of is shown.

Figure 4.—

Posterior distributions of for the Pacific herring between Funka Bay and Miyako Bay at each locus, and over all loci, which were averaged over at five loci.

Figure 5.—

Posterior distributions of for the Pacific herring over all loci, which were averaged over for five loci: AK, Lake Akkeshi; YD, Yudonuma Lake; FK, Funka Bay; OB, Obuchinuma Lake; MY, Miyako Bay; and MT, Matsushima Bay.

Figure 6.—

Confidence regions of the distribution of in the genome of the Pacific herring, assuming a normal distribution (see the text). (A) The confidence regions of μ and σ², which specify the distribution. (B) The MLE distribution (red line, the delta distribution) and the representative distributions on the boundary of the confidence regions (a–e), which correspond to the points in A. The distribution of the weighted mean of is superimposed (blue line).

Figure 6.—

Confidence regions of the distribution of in the genome of the Pacific herring, assuming a normal distribution (see the text). (A) The confidence regions of μ and σ², which specify the distribution. (B) The MLE distribution (red line, the delta distribution) and the representative distributions on the boundary of the confidence regions (a–e), which correspond to the points in A. The distribution of the weighted mean of is superimposed (blue line).