Adaptive regulation of sparseness by feedforward inhibition
- PMID: 17660812
- PMCID: PMC4061731
- DOI: 10.1038/nn1947
Adaptive regulation of sparseness by feedforward inhibition
Abstract
In the mushroom body of insects, odors are represented by very few spikes in a small number of neurons, a highly efficient strategy known as sparse coding. Physiological studies of these neurons have shown that sparseness is maintained across thousand-fold changes in odor concentration. Using a realistic computational model, we propose that sparseness in the olfactory system is regulated by adaptive feedforward inhibition. When odor concentration changes, feedforward inhibition modulates the duration of the temporal window over which the mushroom body neurons may integrate excitatory presynaptic input. This simple adaptive mechanism could maintain the sparseness of sensory representations across wide ranges of stimulus conditions.
Conflict of interest statement
The authors declare no competing financial interests.
Figures





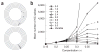
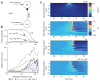
References
-
- Gross-Isseroff R, Lancet D. Concentration-dependent changes of perceived odor quality. Chem Senses. 1988;13:191–204.
-
- Bhagavan S, Smith BH. Olfactory conditioning in the honey bee, Apis mellifera: effects of odor intensity. Physiol Behav. 1997;61:107–117. - PubMed
-
- Stopfer M, Jayaraman V, Laurent G. Intensity versus identity coding in an olfactory system. Neuron. 2003;39:991–1004. - PubMed
-
- Laurent G. Olfactory network dynamics and the coding of multidimensional signals. Nat Rev Neurosci. 2002;3:884–895. - PubMed
-
- Kanerva P. Sparse Distributed Memory. Bradford Books; Boston: 1988.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

