Lock-and-key mechanisms of cerebellar memory recall based on rebound currents
- PMID: 17671105
- PMCID: PMC2576199
- DOI: 10.1152/jn.00344.2007
Lock-and-key mechanisms of cerebellar memory recall based on rebound currents
Abstract
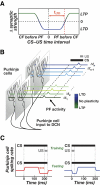
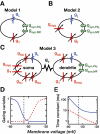
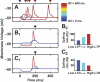
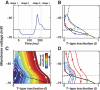
A basic question for theories of learning and memory is whether neuronal plasticity suffices to guide proper memory recall. Alternatively, information processing that is additional to readout of stored memories might occur during recall. We formulate a "lock-and-key" hypothesis regarding cerebellum-dependent motor memory in which successful learning shapes neural activity to match a temporal filter that prevents expression of stored but inappropriate motor responses. Thus, neuronal plasticity by itself is necessary but not sufficient to modify motor behavior. We explored this idea through computational studies of two cerebellar behaviors and examined whether deep cerebellar and vestibular nuclei neurons can filter signals from Purkinje cells that would otherwise drive inappropriate motor responses. In eyeblink conditioning, reflex acquisition requires the conditioned stimulus (CS) to precede the unconditioned stimulus (US) by >100 ms. In our biophysical models of cerebellar nuclei neurons this requirement arises through the phenomenon of postinhibitory rebound depolarization and matches longstanding behavioral data on conditioned reflex timing and reliability. Although CS-US intervals<100 ms may induce Purkinje cell plasticity, cerebellar nuclei neurons drive conditioned responses only if the CS-US training interval was >100 ms. This bound reflects the minimum time for deinactivation of rebound currents such as T-type Ca2+. In vestibulo-ocular reflex adaptation, hyperpolarization-activated currents in vestibular nuclei neurons may underlie analogous dependence of adaptation magnitude on the timing of visual and vestibular stimuli. Thus, the proposed lock-and-key mechanisms link channel kinetics to recall performance and yield specific predictions of how perturbations to rebound depolarization affect motor expression.
Figures



Similar articles
-
Model-Driven Analysis of Eyeblink Classical Conditioning Reveals the Underlying Structure of Cerebellar Plasticity and Neuronal Activity.IEEE Trans Neural Netw Learn Syst. 2017 Nov;28(11):2748-2762. doi: 10.1109/TNNLS.2016.2598190. IEEE Trans Neural Netw Learn Syst. 2017. PMID: 27608482
-
Intrinsic and synaptic plasticity in the vestibular system.Curr Opin Neurobiol. 2006 Aug;16(4):385-90. doi: 10.1016/j.conb.2006.06.012. Epub 2006 Jul 13. Curr Opin Neurobiol. 2006. PMID: 16842990 Review.
-
Learning in a simple motor system.Learn Mem. 2004 Mar-Apr;11(2):127-36. doi: 10.1101/lm.65804. Learn Mem. 2004. PMID: 15054127 Review.
-
Distribution of neural plasticity in cerebellum-dependent motor learning.Prog Brain Res. 2014;210:79-101. doi: 10.1016/B978-0-444-63356-9.00004-2. Prog Brain Res. 2014. PMID: 24916290
-
Memory trace of motor learning shifts transsynaptically from cerebellar cortex to nuclei for consolidation.Neuroscience. 2006 May 12;139(2):767-77. doi: 10.1016/j.neuroscience.2005.12.035. Epub 2006 Feb 3. Neuroscience. 2006. PMID: 16458438
Cited by
-
Decoding brain memory formation by single-cell RNA sequencing.Brief Bioinform. 2022 Nov 19;23(6):bbac412. doi: 10.1093/bib/bbac412. Brief Bioinform. 2022. PMID: 36156112 Free PMC article.
-
Mini-review: synaptic integration in the cerebellar nuclei--perspectives from dynamic clamp and computer simulation studies.Cerebellum. 2011 Dec;10(4):659-66. doi: 10.1007/s12311-011-0248-3. Cerebellum. 2011. PMID: 21259124 Review.
-
Dynamic modulation of activity in cerebellar nuclei neurons during pavlovian eyeblink conditioning in mice.Elife. 2017 Dec 15;6:e28132. doi: 10.7554/eLife.28132. Elife. 2017. PMID: 29243588 Free PMC article.
-
Evolving Models of Pavlovian Conditioning: Cerebellar Cortical Dynamics in Awake Behaving Mice.Cell Rep. 2015 Dec 1;13(9):1977-88. doi: 10.1016/j.celrep.2015.10.057. Epub 2015 Nov 19. Cell Rep. 2015. PMID: 26655909 Free PMC article.
-
Questioning the role of rebound firing in the cerebellum.Nat Neurosci. 2008 Nov;11(11):1256-8. doi: 10.1038/nn.2195. Epub 2008 Sep 28. Nat Neurosci. 2008. PMID: 18820695 Free PMC article.
References
-
- Abbott LF, Nelson SB. Synaptic plasticity: taming the beast. Nat Neurosci Suppl 3: 1178–1183, 2000. - PubMed
-
- Aizenman CD, Linden DJ. Regulation of the rebound depolarization and spontaneous firing patterns of deep nuclear neurons in slices of rat cerebellum. J Neurophysiol 82: 1697–1709, 1999. - PubMed
-
- Aizenman CD, Linden DJ. Rapid, synaptically driven increases in the intrinsic excitability of cerebellar deep nuclear neurons. Nat Neurosci 3: 109–111, 2000. - PubMed
-
- Aizenman CD, Manis PB, Linden DJ. Polarity of long-term synaptic gain change is related to postsynaptic spike firing at a cerebellar inhibitory synapse. Neuron 21: 827–835, 1998. - PubMed
-
- Aksenov DP, Serdyukova NA, Bloedel JR, Bracha V. Glutamate neurotransmission in the cerebellar interposed nuclei: involvement in classically conditioned eyeblinks and neuronal activity. J Neurophysiol 93: 44–52, 2005. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Miscellaneous

