Brain surface conformal parameterization using Riemann surface structure

Abstract

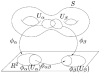
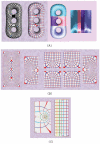
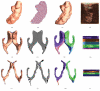
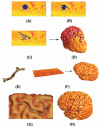
In medical imaging, parameterized 3-D surface models are useful for anatomical modeling and visualization, statistical comparisons of anatomy, and surface-based registration and signal processing. Here we introduce a parameterization method based on Riemann surface structure, which uses a special curvilinear net structure (conformal net) to partition the surface into a set of patches that can each be conformally mapped to a parallelogram. The resulting surface subdivision and the parameterizations of the components are intrinsic and stable (their solutions tend to be smooth functions and the boundary conditions of the Dirichlet problem can be enforced). Conformal parameterization also helps transform partial differential equations (PDEs) that may be defined on 3-D brain surface manifolds to modified PDEs on a two-dimensional parameter domain. Since the Jacobian matrix of a conformal parameterization is diagonal, the modified PDE on the parameter domain is readily solved. To illustrate our techniques, we computed parameterizations for several types of anatomical surfaces in 3-D magnetic resonance imaging scans of the brain, including the cerebral cortex, hippocampi, and lateral ventricles. For surfaces that are topologically homeomorphic to each other and have similar geometrical structures, we show that the parameterization results are consistent and the subdivided surfaces can be matched to each other. Finally, we present an automatic sulcal landmark location algorithm by solving PDEs on cortical surfaces. The landmark detection results are used as constraints for building conformal maps between surfaces that also match explicitly defined landmarks.

Fig. 1

Structure of a manifold. An atlas is a family of charts that jointly form an open covering of the manifold [25].

Fig. 2

(A) Conformal net and critical graph of a closed three-hole torus surface. There are four zero points. The critical horizontal trajectories partition the surface to four topological cylinders, color encoded in the third frame. Each cylinder is conformally mapped to a planar rectangle. (B) Conformal net and critical graph of a open boundary four-hole annulus on the plane. There are three zero points; the critical horizontal trajectories partition the surface to six topological disks. (C). Each segment is conformally mapped to a rectangle. The trajectories and the boundaries are color encoded and the corners are labelled. (Pictures are adapted from [29].)

Fig. 3

The holomorphic flow segmentation results of (a)–(d) a hippocampal surface and (e)–(l) two lateral ventricular surfaces. (b) is the conformal net of the hippocampal surface in (a). (c) is an isoparameter curve used to unfold the surface. (d) is the rectangle to which the surface is conformally mapped. (e)–(h) show lateral ventricles parameterized using holomorphic 1-forms for a 65-year-old subject with HIV/AIDS; (i)–(l) show the same maps computed for a healthy 21-year-old control subject. (e) and (i) show that five cuts are automatically introduced and convert the lateral ventricular surface into a genus 4 surface. Other pictures show the (f) and (j) computed conformal net, (g) and (k) holomorphic flow segmentation, and (h) and (l) their associated parameter domains (the texture mapped into the parameter domain here simply corresponds to the intensity of the surface rendering, which is based on the surface normals).

Fig. 4

Illustrates the parameterization of cortical surfaces using the holomorphic 1-form approach. The thick lines are landmark curves, including several major sulci lying in the cortical surface. These sulcal curves are always mapped to a boundary in the parameter space images.

Fig. 5

(A)–(D) show sulcal curve extraction on the cortical surface by the CV segmentation. With a suitable initial contour, major sulcal landmarks can be effectively extracted at the same time. (E) shows how umbilic points are located within each candidate sulci region, and these are then chosen as the end points of the landmark curves. When multiple candidates regions are located, we select the two regions that are farthest apart. (F)–(H) illustrate automatic landmark tracking using a variational approach. In (F), we track the landmark curves on the parameter domain along the edges whose directions are closest to the principal direction field. The corresponding landmark curves on the cortical surface are shown. This gives a good initialization for our variational method to locate landmarks. (G) demonstrates that landmarks curve is evolved to a deeper region using our variational approach. The blue and green curves represents the initial and evolved curves, respectively. (H) shows ten sulci landmarks that are detected and tracked using our algorithm.

Fig. 6

An average cortical surface of the brain derived by using optimized conformal parametrization with the automatically traced landmarks. The major sulcal landmarks are well preserved (see the areas inside green circles in (B) and (C). In (D), the sulci at the back of the brain, in the occipital lobe surface, are averaged out because no landmark constraint was added in that region, for purposes of illustration.