Assessing uncertainty in spatial exposure models for air pollution health effects assessment

Abstract

Background: Although numerous epidemiologic studies now use models of intraurban exposure, there has been little systematic evaluation of the performance of different models.

Objectives: In this present article we proposed a modeling framework for assessing exposure model performance and the role of spatial autocorrelation in the estimation of health effects.

Methods: We obtained data from an exposure measurement substudy of subjects from the Southern California Children's Health Study. We examined how the addition of spatial correlations to a previously described unified exposure and health outcome modeling framework affects estimates of exposure-response relationships using the substudy data. The methods proposed build upon the previous work, which developed measurement-error techniques to estimate long-term nitrogen dioxide exposure and its effect on lung function in children. In this present article, we further develop these methods by introducing between- and within-community spatial autocorrelation error terms to evaluate effects of air pollution on forced vital capacity. The analytical methods developed are set in a Bayesian framework where multistage models are fitted jointly, properly incorporating parameter estimation uncertainty at all levels of the modeling process.

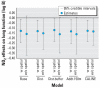
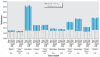
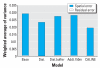
Results: Results suggest that the inclusion of residual spatial error terms improves the prediction of adverse health effects. These findings also demonstrate how residual spatial error may be used as a diagnostic for comparing exposure model performance.

Figure 1

Location map of communities in CHS study. All communities are located in Southern California (see inset)

Figure 2

Directed acyclic graph (DAG) for entire model.

Figure 3

Spatial versus nonspatial effects across models. Abbreviations: w, with; w/o, without.

Figure 4

Variances of the individual-level spatial and independent residual terms for each California community in the exposure model Equation 2 for different choices of exposure predictors. (See text for definition of the variances plotted.) Numbers in parentheses indicate sample size.

Figure 5

Variances of the individual-level spatial and independent residual terms for each community in the lung function model Equation 1 for different choices of exposure predictors. (See text for definition of the variances plotted.)

Figure 6

Variances of the community-level spatial and independent residual terms in the exposure model Equation 5 for different choices of exposure predictors. (See text for definition of the variances plotted.)

Figure 7

Variances of the community-level spatial and independent residual terms in the lung function model Equation 4 for different choices of exposure predictors. (See text for definition of the variances plotted.)

Figure 8

Comparison of different levels of NO₂.