Using the logarithm of odds to define a vector space on probabilistic atlases

Abstract

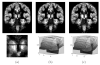
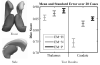
The logarithm of the odds ratio (LogOdds) is frequently used in areas such as artificial neural networks, economics, and biology, as an alternative representation of probabilities. Here, we use LogOdds to place probabilistic atlases in a linear vector space. This representation has several useful properties for medical imaging. For example, it not only encodes the shape of multiple anatomical structures but also captures some information concerning uncertainty. We demonstrate that the resulting vector space operations of addition and scalar multiplication have natural probabilistic interpretations. We discuss several examples for placing label maps into the space of LogOdds. First, we relate signed distance maps, a widely used implicit shape representation, to LogOdds and compare it to an alternative that is based on smoothing by spatial Gaussians. We find that the LogOdds approach better preserves shapes in a complex multiple object setting. In the second example, we capture the uncertainty of boundary locations by mapping multiple label maps of the same object into the LogOdds space. Third, we define a framework for non-convex interpolations among atlases that capture different time points in the aging process of a population. We evaluate the accuracy of our representation by generating a deformable shape atlas that captures the variations of anatomical shapes across a population. The deformable atlas is the result of a principal component analysis within the LogOdds space. This atlas is integrated into an existing segmentation approach for MR images. We compare the performance of the resulting implementation in segmenting 20 test cases to a similar approach that uses a more standard shape model that is based on signed distance maps. On this data set, the Bayesian classification model with our new representation outperformed the other approaches in segmenting subcortical structures.

Fig. 1

The MR image on the top shows the right superior temporal gyrus. The corresponding segmentations by six experts (A - F) are shown below. Significant difference between the segmentations are visible. The third row shows the corresponding signed distance maps that can capture the boundary of each segmentation but not the uncertainty about the boundary location across the raters.

Fig. 2

Displaying the impact of α ∈ ℙ on the results of the probabilistic scalar multiplication ⊛ with a PA. The first row shows a 2D PA. The result of the operation with α = 0.5 and α = 2 are shown in the second row. When α is small the slope of the PA is gentle, indicating higher uncertainty of the boundary location as also shown by the graph of the corresponding entropy in the third row. When α is large the slope steepens and the entropy is characterized by a thinner ridge.

Fig. 3

The first row shows two binary maps and a multicategorical label map. The corresponding SDMs are shown in the second row. The contours nicely preserve the original shape. The third row shows the LogOdds map defined by the logit function of the Gaussian smoothed binary maps (GAUSS) (see third row of Figure 4). These maps are very similar to the SDMs for the binary maps. For the label map of the two circles (Light Gray and Dark Gray), however, the corresponding contours of the LogOdds maps are influenced by the neighboring circle.

Fig. 4

The first row shows the binary and label maps of Figure 3. The second and third rows are the PAs generated from the SDMs in Figure 3 (second row) and the PA defined by Gaussian smoothing of the binary maps (GAUSS). While the contours of GAUSS preserve the original shape, the PAs generated from SDMs do not for the label map of the two circles (Light Gray and Dark Gray). Thus, in this example, SDMs are not well suited for capturing uncertainty about boundary location.

Fig. 5

The performance of each of the six expert segmentations is represented by a Gaussian cumulative function (left graph). The ideal distribution is a step function (shown in light gray). Their corresponding log odds map generated using Equation (2) can be observed on the right. Dark blue and dark red indicates high certainty that the voxel is assigned to the background and foreground respectively. All other colors represent statistical uncertainty about the assignment of the voxel.

Fig. 6

The graph to the left shows the probabilistic atlas of a population at time point 0 and 1. The atlas is characterized by a Gaussian distribution in space with mean A at time point 0 and B at time point 1. The result of the convex combination of these distributions at time point 0.5 resembles a multimodal distribution in ${\mathbb{P}}_2^n$ and a normal distribution in ${\mathbb{L}}_1^n$.

Fig. 7

The first row shows a sample slice of an interpolation of a longitudinal schizophrenia study. Each image represents a PA of the gray matter at a specific point in time of the study. Bright indicates high and dark low probability of the gray matter. The second row shows the PA of the thalamus (a) with black indicating the voxels that are interpolated over three time point in (b) and (c). Graph (b) was produced by linear interpolation, while the smoother quadratic spline interpolation is shown in (c).

Fig. 8

Different views of a 3D model of the thalamus (dark gray) and the caudate (light gray). The model is based on a segmentation generated by EM-𝒫. The graph to the right summarizes the results of our experiment. For both structures EM-𝒫 performs much better than EM-ℋ and EM-N.