Using the logarithm of odds to define a vector space on probabilistic atlases
- PMID: 17698403
- PMCID: PMC2423493
- DOI: 10.1016/j.media.2007.06.003
Using the logarithm of odds to define a vector space on probabilistic atlases
Abstract
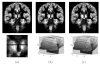
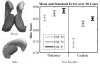
The logarithm of the odds ratio (LogOdds) is frequently used in areas such as artificial neural networks, economics, and biology, as an alternative representation of probabilities. Here, we use LogOdds to place probabilistic atlases in a linear vector space. This representation has several useful properties for medical imaging. For example, it not only encodes the shape of multiple anatomical structures but also captures some information concerning uncertainty. We demonstrate that the resulting vector space operations of addition and scalar multiplication have natural probabilistic interpretations. We discuss several examples for placing label maps into the space of LogOdds. First, we relate signed distance maps, a widely used implicit shape representation, to LogOdds and compare it to an alternative that is based on smoothing by spatial Gaussians. We find that the LogOdds approach better preserves shapes in a complex multiple object setting. In the second example, we capture the uncertainty of boundary locations by mapping multiple label maps of the same object into the LogOdds space. Third, we define a framework for non-convex interpolations among atlases that capture different time points in the aging process of a population. We evaluate the accuracy of our representation by generating a deformable shape atlas that captures the variations of anatomical shapes across a population. The deformable atlas is the result of a principal component analysis within the LogOdds space. This atlas is integrated into an existing segmentation approach for MR images. We compare the performance of the resulting implementation in segmenting 20 test cases to a similar approach that uses a more standard shape model that is based on signed distance maps. On this data set, the Bayesian classification model with our new representation outperformed the other approaches in segmenting subcortical structures.
Figures






References
-
- Arsigny V, Fillard P, Pennec X, Ayache N. Geometric means in a novel vector space structure on symmetric positive-definite matrices. SIAM Journal on Matrix Analysis and Applications. 2007;29:328–347.
-
- Ashburner J, Friston K. Voxel-based morphometry - the methods. NeuroImage. 2000;11:805–821. - PubMed
-
- Ashburner J, Friston K. Unified segmentation. NeuroImage. 2005;26(3):839–851. - PubMed
-
- Besag J. On the statistical analysis of dirty pictures. (Series B).Journal of the Royal Society. 1986;48(3):259–302.
-
- Bookstein F. Landmark methods for forms without landmarks: morphometrics of group differences in outline shape. Medical Image Analysis. 1996;1(3):225–243. - PubMed
Publication types
MeSH terms
Grants and funding
- P41-RR13218/RR/NCRR NIH HHS/United States
- K05 MH070047/MH/NIMH NIH HHS/United States
- U41 RR019703/RR/NCRR NIH HHS/United States
- R01 MH 50747/MH/NIMH NIH HHS/United States
- P41 RR013218/RR/NCRR NIH HHS/United States
- R01 MH 40799/MH/NIMH NIH HHS/United States
- U24-RR021382/RR/NCRR NIH HHS/United States
- 27302C0031/ES/NIEHS NIH HHS/United States
- U24 RR021382/RR/NCRR NIH HHS/United States
- R01 MH040799/MH/NIMH NIH HHS/United States
- R01-NS051826/NS/NINDS NIH HHS/United States
- R01 AA016748/AA/NIAAA NIH HHS/United States
- U54 EB005149/EB/NIBIB NIH HHS/United States
- K05 MH 70047/MH/NIMH NIH HHS/United States
- U41-RR019703/RR/NCRR NIH HHS/United States
- R01 NS051826/NS/NINDS NIH HHS/United States
LinkOut - more resources
Full Text Sources
Medical

