Evaluating and learning from RNA pseudotorsional space: quantitative validation of a reduced representation for RNA structure

Abstract

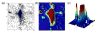
Quantitatively describing RNA structure and conformational elements remains a formidable problem. Seven standard torsion angles and the sugar pucker are necessary to characterize the conformation of an RNA nucleotide completely. Progress has been made toward understanding the discrete nature of RNA structure, but classifying simple and ubiquitous structural elements such as helices and motifs remains a difficult task. One approach for describing RNA structure in a simple, mathematically consistent, and computationally accessible manner involves the invocation of two pseudotorsions, eta (C4'(n-1), P(n), C4'(n), P(n+1)) and theta (P(n), C4'(n), P(n+1), C4'(n+1)), which can be used to describe RNA conformation in much the same way that varphi and psi are used to describe backbone configuration of proteins. Here, we conduct an exploration and statistical evaluation of pseudotorsional space and of the Ramachandran-like eta-theta plot. We show that, through the rigorous quantitative analysis of the eta-theta plot, the pseudotorsional descriptors eta and theta, together with sugar pucker, are sufficient to describe RNA backbone conformation fully in most cases. These descriptors are also shown to contain considerable information about nucleotide base conformation, revealing a previously uncharacterized interplay between backbone and base orientation. A window function analysis is used to discern statistically relevant regions of density in the eta-theta scatter plot and then nucleotides in colocalized clusters in the eta-theta plane are shown to have similar 3-D structures through RMSD analysis of the RNA structural constituents. We find that major clusters in the eta-theta plot are few, underscoring the discrete nature of RNA backbone conformation. Like the Ramachandran plot, the eta-theta plot is a valuable system for conceptualizing biomolecular conformation, it is a useful tool for analyzing RNA tertiary structures, and it is a vital component of new approaches for solving the 3-D structures of large RNA molecules and RNA assemblies.

Figure 1

(a) Diagram of a nucleotide showing the standard backbone torsional angles. (b) Diagram depicting the definitions of the pseudotorsions, η and θ. The red lines indicate the pseudo-bonds that connect successive P and C4’ atoms. The portion of the backbone shown is that which affects a single pair of η and θ values, as the pseudotorsions extend into the previous and next nucleotide. In both diagrams, the P and C4’ atoms are shown in red and labeled for reference.

Figure 2

The effect of windowing an η−θ plot with a Blackman window function of width 60°. (a) An η−θ scatter plot of all nucleotides from our data set. Each point shows the η and θ values of an individual nucleotide. (b) The result of applying the Blackman window to the data set, colored from low to high density: blue, green, yellow, and red. (c) A 3-dimensional representation of the data set with a Blackman window function applied. An upper cutoff has been applied to allow for better discerning of the peaks surrounding the helical region.

Figure 3

Scatter plots of RMSD versus distance in the η−θ plane or standard torsional angles for 10,000 random pairs of nucleotides from the data set. For each plot, the best fit line is shown on the plot. (a) RMSD of backbone atoms versus distance in the η-θ plane. The correlation coefficient is 0.80. (b) RMSD of backbone atoms versus distance of standard torsional backbone angles. The correlation coefficient is 0.50. (c) RMSD of backbone, sugar, and base atoms versus distance in the η-θ plane. The correlation coefficient is 0.81. (d) RMSD of backbone, sugar, and base atoms versus distance of the standard torsional angles (including χ). The correlation coefficient is 0.50.

Figure 4

Cluster analysis of the plot of non-helical C3’-endo nucleotides. (a) A scatter plot of the η−θ values of all C3’-endo nucleotides. (b) A 3-dimensional view of the plot of C3’-endo nucleotides with a 60° wide Blackman window function applied. (c) A contour plot and the results of analyzing the density plot. Contour levels are shown for ρ̄ + 1σ, ρ̄ + 2σ, and ρ̄ + 4σ, and scores are given in that order. Contours with small populations (<9) are not shown. The blue bars span the helical η values and the helical θ values. The pink, elliptical area near the center of plot indicates the helical region and was initially excluded from the analysis. (d-i) Prototype nucleotides corresponding to the clusters labeled in (c). Portions of the previous and next nucleotide that affect the pseudotorsions are also shown.

Figure 5

Cluster analysis of the plot of C2’-endo nucleotides. (a) A scatter plot of the η−θ values of all C2’-endo nucleotides. (b) A 3-dimensional view of the plot of C2’-endo nucleotides with a 60° wide Blackman window function applied. (c) A contour plot and the results of analyzing the density plot. Contour levels are shown for ρ̄ + 1σ, ρ̄ + 2σ, and ρ̄ + 4σ, and scores are given in that order. Contours with small populations (<9) are not shown. (d-g) Prototype nucleotides corresponding to the clusters labeled in (c). Portions of the previous and next nucleotide that affect the pseudotorsions are also shown.

Figure 6

Cluster scores using both backbone and base atoms for (a) non-helical C3’-endo nucleotides and (b) C2’ endo nucleotides. Clusters are identical to those shown in Figures 4 and 5 and were determined using only backbone atoms.

Figure 7

Strands built using only η and θ (a) An example of an in silico tetraloop (blue) superimposed on the original (1S72 0:89-94) (red). (b) A bulge region (1S72 0:1391-1398) from a 50S ribosomal subunit was built (blue) and superimposed on the original (red).